题目内容
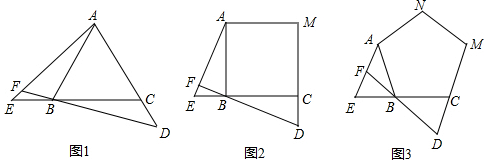
11.探究:如图1,△ABC是等边三角形,在边CB、AC的延长线上截取BE=CD,连结BD、AE,延长DB交AE于点F.(1)求证:△BAE≌△CBD;
(2)∠BFE=120°.
应用:将图1的△ABC分别改为正方形ABCM和正五边形ABCMN,如图2、3,在边CB、MC的延长线上截取BE=CD,连结BD、AE,延长DB交AE于点F,则图2中∠BFE=90°;图3中∠BFE=72°.
拓展:若将图1的△ABC改为正n边形,其它条件不变,则∠BFE==($\frac{360}{n}$)°(用含n的代数式表示).
分析 探究:(1)根据△BCA是等边三角形,得出BC=AB,∠ACB=∠ABC=60°,进而得到∠BCD=∠ABE=120°,从而得到△CBD≌△BAE(SAS);(2)利用全等三角形的性质得到对应角相等,再利用三角形的内角和定理,即可得出∠BFE=∠BCD,进而得解;
应用:利用正方形(或正五边形)的性质得到BC=AB,∠BCD=∠ABE,从而判断出△CBD≌△BAE(SAS);再利用全等三角形的性质得到∠CDN=∠BCM,再利用全等三角形的性质得到对应角相等,再利用三角形的内角和定理,即可得出∠BFE=∠BCD,进而得解;
拓展:利用相同的方法可得出全等三角形,再利用全等三角形的性质得到对应角相等,再利用三角形的内角和,即可得出∠BFE的度数为正n边形的外角度数.
解答  探究:(1)解:∵△BCA是等边三角形,
探究:(1)解:∵△BCA是等边三角形,
∴BC=AB,∠ACB=∠ABC=60°,
∴∠BCD=∠ABE=120°,
在△CBD和△BAE中,
$\left\{\begin{array}{l}{BC=AB}\\{∠BCD=∠ABE}\\{CD=BE}\end{array}\right.$,
∴△CBD≌△BAE(SAS);
(2)解:∵△CBD≌△BAE,
∴∠E=∠D,
∵∠EBF=∠DBC,
∴∠BFE=∠BCD,
又∵∠BCD=180°-60°=120°,
∴∠BFE=120°,
故答案为120;
应用:图2中,根据SAS易证△CBD≌△BAE,
∴∠E=∠D,
∵∠EBF=∠DBC,
∴∠BFE=∠BCD,
又∵∠BCD=180°-90°=90°,
∴∠BFE=90°,
图3中,根据SAS易证△CBD≌△BAE,
∴∠E=∠D,
∵∠EBF=∠DBC,
∴∠BFE=∠BCD,
又∵∠BCD=180°-108°=72°,
∴∠BFE=72°,
故答案为90°;72°.
拓展:若将图1的△ABC改为正n边形,其它条件不变,则∠BFE的度数为正n边形的外角度数,
即∠BFE=($\frac{360}{n}$)°,
故答案为:($\frac{360}{n}$)°
点评 本题是四边形的综合题,也是一道规律题,主要考查了正n边形的性质,解题时需要运用等边三角形、正方形、正五边形的性质以及全等三角形的性质和判定,三角形的内角和定理等,解题的关键是利用全等三角形的对应角相等以及三角形内角和定理进行推导,并找出规律.

| A. | 如果两个三角形全等,则它们一定能关于某直线成轴对称 | |
| B. | 如果两个三角形关于某直线成轴对称,那么它们是全等三角形 | |
| C. | 等腰三角形的对称轴是底边上的高 | |
| D. | 若两个图形关于某直线对称,则它们的对应点一定位于对称轴的两侧 |
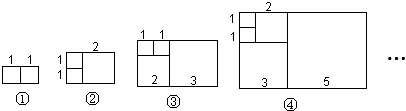
每个长方形的周长如表所示:
| 序号 | ① | ② | ③ | ④ | … |
| 周长 | 6 | 10 | x | y | … |
(2)若按此规律继续拼长方形,则序号为⑩的长方形周长是466.
| A. | -3a2 | B. | -3a3 | C. | 3a2 | D. | 3a |
| A. | y=2(x+2)2+1 | B. | y=2(x-2)2+1 | C. | y=2(x+2)2-1 | D. | y=2(x-2)2-1 |



