题目内容
20.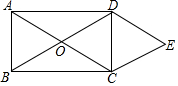 如图,矩形ABCD的对角线AC与BD相交于点O,CE∥BD,DE∥AC,AD=2$\sqrt{3}$,DE=2,下列结论:①AB=2;②∠E=45°;③四边形OCED是菱形;④四边形OCED的面积为2$\sqrt{3}$,其中正确的是①③④(把所有正确结论的序号都填上).
如图,矩形ABCD的对角线AC与BD相交于点O,CE∥BD,DE∥AC,AD=2$\sqrt{3}$,DE=2,下列结论:①AB=2;②∠E=45°;③四边形OCED是菱形;④四边形OCED的面积为2$\sqrt{3}$,其中正确的是①③④(把所有正确结论的序号都填上).
分析 依据矩形的性质可知OC=OD,然后依据平行四边形的定义可知四边形OCED是平行四边形,从而可证明四边形OCED是菱形故此可对③作出判断,由菱形的性质可得到OC=2,从而可求得AC的长,然后依据勾股定理可求得DC的长则可对①作出判断,由DE=CE=DC=2,可求得∠E的度数,故此可对②作出判断,连接OE,可证明四边形OBCE为平行四边形,从而可求得OE=2$\sqrt{3}$,最后依据菱形的面积等于两对角线乘积的一半可求得菱形OCED的面积.
解答 解:∵CE∥BD,DE∥AC,
∴四边形OCED是平行四边形,
∴OD=EC,OC=DE.
∵矩形ABCD的对角线AC与BD相交于点O,
∴OD=OC.
∴四边形OCED是菱形,故③正确.
∵DE=2,
∴AC=2OC=2DE=4,
∴AB=DC=$\sqrt{A{C}^{2}-A{D}^{2}}$=$\sqrt{{4}^{2}-(2\sqrt{3})^{2}}$=2,故①正确.
∴ED=DC=CE=2,
∴∠E=60°,故②错误.
如图所示:连接OE.
∵OB∥CE且OB=CE,
∴四边形OBCE为平行四边形.
∴OE=BC=2$\sqrt{3}$.
∴四边形OCED的面积=$\frac{1}{2}$DC•OE=$\frac{1}{2}$×2×2$\sqrt{3}$=2$\sqrt{3}$,故④正确.
故答案为:①③④.
点评 本题主要考查的是矩形的性质、菱形、平行四边形的判定和性质、等边三角形的判定和性质,掌握本题的辅助线的作法是解题的关键.

练习册系列答案
相关题目
9.已知函数y=ax2-2ax-1(a是常数,a≠0),下列结论正确的是( )
| A. | 当a=1时,函数图象过点(-1,1) | |
| B. | 当a=-2时,函数图象与x轴没有交点 | |
| C. | 若a>0,则当x≥1时,y随x的增大而减小 | |
| D. | 不论a为何值,函数图象必经过(2,-1) |
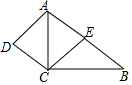 如图,在四边形ABCD中,AB∥CD,AC平分∠BAD,CE∥AD交AB于点E.
如图,在四边形ABCD中,AB∥CD,AC平分∠BAD,CE∥AD交AB于点E.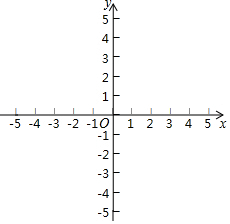 已知一次函数y1=k1x+b1的图象过点M(-1,6),Q(3,-2),一次函数y2=k2x+b2的图象过点N(-3,-6),P(3,6).
已知一次函数y1=k1x+b1的图象过点M(-1,6),Q(3,-2),一次函数y2=k2x+b2的图象过点N(-3,-6),P(3,6).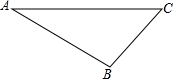 如图,已知△ABC
如图,已知△ABC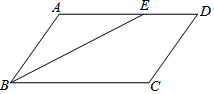 如图,在?ABCD中,ED=2,BC=5,∠ABC的平分线交AD于点E,则AB的长为3.
如图,在?ABCD中,ED=2,BC=5,∠ABC的平分线交AD于点E,则AB的长为3.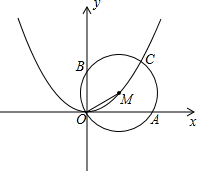 如图,M是抛物线y=ax2(a>0)上一点,以MO为半径画⊙M交x轴于点A(2,0),交y轴于点B,交抛物线于另一点C.若$\widehat{CA}$=$\widehat{CB}$,则a=$\frac{-1+\sqrt{5}}{2}$.
如图,M是抛物线y=ax2(a>0)上一点,以MO为半径画⊙M交x轴于点A(2,0),交y轴于点B,交抛物线于另一点C.若$\widehat{CA}$=$\widehat{CB}$,则a=$\frac{-1+\sqrt{5}}{2}$.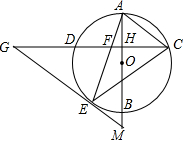 如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,连结AC,过$\widehat{BD}$上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.
如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,连结AC,过$\widehat{BD}$上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.