题目内容
15.(1)解方程:a2+4a-2=0;(2)解不等式组:$\left\{\begin{array}{l}2x+1>-1\\ 4x-3≤2-x\end{array}\right.$.
分析 (1)移项,配方,开方,即可得出两个一元一次方程,求出方程的解即可;
(2)先求出每个不等式的解集,再求出不等式组的解集即可.
解答 解:(1)a2+4a-2=0,
a2+4a=2,
a2+4a+4=2+4,
(a+2)2=6,
a+2=$±\sqrt{6}$,
解得:a1=-2+$\sqrt{6}$,a2=-2-$\sqrt{6}$;
(2)$\left\{\begin{array}{l}{2x+1>-1①}\\{4x-3≤2-x②}\end{array}\right.$
解不等式①,得x>-1,
解不等式②,得x≤1,
所以不等式组的解集是-1<x≤1.
点评 本题考查了解一元一次不等式组和解一元二次方程的应用,解(1)小题的关键是能正确配方,解(2)小题的关键是能根据不等式的解集找出不等式组的解集.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案
相关题目
3.下列命题是假命题的是( )
| A. | 菱形的对角线互相垂直平分 | |
| B. | 有一斜边与一直角边对应相等的两直角三角形全等 | |
| C. | 有一组邻边相等且垂直的平行四边形是正方形 | |
| D. | 对角线相等的四边形是矩形 |
7. 如图,在?ABCD中,AB=6,AD=8,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于G,BG=4$\sqrt{2}$,则四边形AECD的周长为( )
如图,在?ABCD中,AB=6,AD=8,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于G,BG=4$\sqrt{2}$,则四边形AECD的周长为( )
 如图,在?ABCD中,AB=6,AD=8,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于G,BG=4$\sqrt{2}$,则四边形AECD的周长为( )
如图,在?ABCD中,AB=6,AD=8,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于G,BG=4$\sqrt{2}$,则四边形AECD的周长为( )| A. | 20 | B. | 21 | C. | 22 | D. | 23 |
4.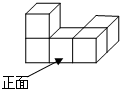 如图是五个相同的正方体组成的一个几何体,则其俯视图是( )
如图是五个相同的正方体组成的一个几何体,则其俯视图是( )
 如图是五个相同的正方体组成的一个几何体,则其俯视图是( )
如图是五个相同的正方体组成的一个几何体,则其俯视图是( )| A. | 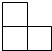 | B. | 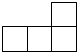 | C. | 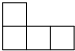 | D. |  |