题目内容
15.关于x的方程$\frac{2}{x-1}=\frac{ax-1}{x(x-1)}$-2有增根,则a=1.分析 增根是化为整式方程后产生的不适合分式方程的根.所以应先确定增根的可能值,让最简公分母(x-5)(x-6)=0,得到x=5或6,然后代入化为整式方程的方程算出a的值.
解答 解:方程两边都乘x(x-1),
得2(x-1)=ax-1-2x(x-1)
∵原方程有增根,
∴最简公分母x(x-1)=0,
解得x=0或1,
当x=0时,不是方程.
当x=1时,a=1,故a的值可能是1,
故答案为:1.
点评 本题考查了分式方程的增根,增根问题可按如下步骤进行:让最简公分母为0确定增根;化分式方程为整式方程;把增根代入整式方程即可求得相关字母的值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5. 如图所示,在△ABC中,已知点D,E,F分别为边BC,AD,CE 的中点,且S△ABC=8cm2,则S阴影面积等于( )
如图所示,在△ABC中,已知点D,E,F分别为边BC,AD,CE 的中点,且S△ABC=8cm2,则S阴影面积等于( )
 如图所示,在△ABC中,已知点D,E,F分别为边BC,AD,CE 的中点,且S△ABC=8cm2,则S阴影面积等于( )
如图所示,在△ABC中,已知点D,E,F分别为边BC,AD,CE 的中点,且S△ABC=8cm2,则S阴影面积等于( )| A. | 4cm2 | B. | 3cm2 | C. | 2cm2 | D. | 1cm2 |
7.已知$\frac{x}{{{x^2}+x+1}}=\frac{1}{8}$(0<x<1).则$\sqrt{x}-\frac{1}{{\sqrt{x}}}$的值为( )
| A. | $-\sqrt{7}$ | B. | $\sqrt{7}$ | C. | $-\sqrt{5}$ | D. | $\sqrt{5}$ |

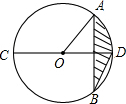 如图,CD是⊙O的直径,弦AB⊥CD,∠ABD=30°,若$CD=2\sqrt{6}$,则阴影部分图形的面积为π.
如图,CD是⊙O的直径,弦AB⊥CD,∠ABD=30°,若$CD=2\sqrt{6}$,则阴影部分图形的面积为π.