题目内容
已知:如图,抛物线y=ax2+bx+2与x轴的交点是A(3,0)、B(6,0),与y轴的交点是C.

(1)求抛物线的函数关系式;
(2)设P(x,y)(0<x<6)是抛物线上的动点,过点P作PQ∥y轴交直线BC于点Q.
①当x取何值时,线段PQ长度取得最大值?其最大值是多少?
②是否存在点P,使△OAQ为直角三角形?若存在,求点P坐标;若不存在,说明理由.

(1)求抛物线的函数关系式;
(2)设P(x,y)(0<x<6)是抛物线上的动点,过点P作PQ∥y轴交直线BC于点Q.
①当x取何值时,线段PQ长度取得最大值?其最大值是多少?
②是否存在点P,使△OAQ为直角三角形?若存在,求点P坐标;若不存在,说明理由.
(1)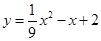 ;(2)①x=3,1;②P(3,0)或
;(2)①x=3,1;②P(3,0)或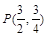 或
或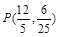 .
.
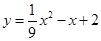 ;(2)①x=3,1;②P(3,0)或
;(2)①x=3,1;②P(3,0)或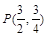 或
或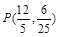 .
.试题分析:(1)由抛物线过A(3,0),B(6,0)即可根据待定系数法列方程组求解;
(2)①先求得抛物线与y轴的交点C的坐标,再求得直线BC的函数表达式,即可表示出线段PQ的长关于x的函数关系式,再根据二次函数的性质求解即可;
②当
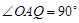 时,点P与点A重合,则P(3,0) ;当
时,点P与点A重合,则P(3,0) ;当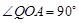 时,点P与点C重合,则x=0(不合题意);当
时,点P与点C重合,则x=0(不合题意);当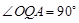 时,设PQ与
时,设PQ与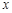 轴交于点D,先根据同角的余角相等证得△ODQ∽△QDA,根据相似三角形的性质可得
轴交于点D,先根据同角的余角相等证得△ODQ∽△QDA,根据相似三角形的性质可得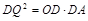 ,即可得到关于x的方程,从而求得结果.
,即可得到关于x的方程,从而求得结果.(1)∵抛物线过A(3,0),B(6,0),
∴
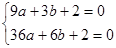 ,解得:
,解得: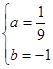
∴抛物线函数表达式是
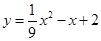 ;
;(2)①∵当x=0时,y=2,
∴点C的坐标为(0,2).
设直线BC的函数表达式是
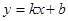 ,
,则有
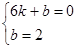 ,解得
,解得 ,
,∴直线BC的函数表达式是y=
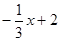
∵0<x<6,
∴PQ=
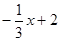 -(
-(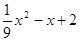 )=
)=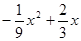 =
= .
.∴当x=3时,线段PQ的长度取得最大值1;
②当
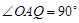 时,点P与点A重合,∴P(3,0)
时,点P与点A重合,∴P(3,0) 当
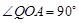 时,点P与点C重合,∴x=0(不合题意)
时,点P与点C重合,∴x=0(不合题意)当
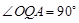 时,设PQ与
时,设PQ与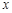 轴交于点D.
轴交于点D. 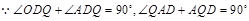 ,
,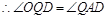 .
.又
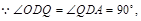
∴△ODQ∽△QDA.
∴
 ,即
,即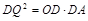 .
.∴
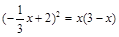 ,
,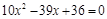 ,
,∴
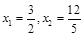 .
. ∴
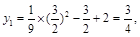
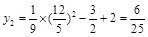 .
.∴
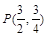 或
或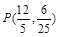 .
.∴所求的点P的坐标是P(3,0)或
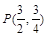 或
或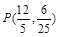 .
.点评:此类问题综合性强,难度较大,在中考中比较常见,一般作为压轴题,题目比较典型.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
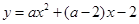 过点
过点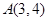 .
. 下方的部分沿直线
下方的部分沿直线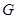 .点
.点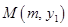 在图象
在图象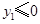 .
.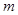 的取值范围;
的取值范围;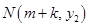 也在图象
也在图象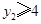 恒成立,则
恒成立,则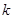 的取值范围为 .
的取值范围为 . 的图像与x轴、y轴的公共点分别为A(5,0)、B,点C在这个二次函数的图像上,且横坐标为3.
的图像与x轴、y轴的公共点分别为A(5,0)、B,点C在这个二次函数的图像上,且横坐标为3.
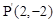 ,点A的对应点为
,点A的对应点为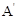 ,则抛物线上PA段扫过的区域(阴影部分)的面积为 .
,则抛物线上PA段扫过的区域(阴影部分)的面积为 .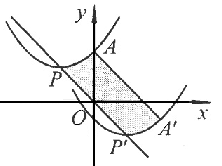
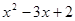 >0.解:令y=
>0.解:令y=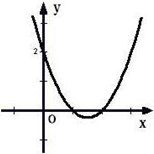
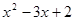 <0的解集为 ;
<0的解集为 ;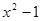 >0的解集为 ;
>0的解集为 ;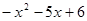 >0.
>0. 的自变量x的取值范围是 .
的自变量x的取值范围是 . 的图象如图所示,则下列结论:①
的图象如图所示,则下列结论:① ;②
;② ;③当
;③当 时,
时, 的最小值为
的最小值为 ,④
,④ 中,正确的有 .
中,正确的有 .
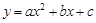 ,使它同时具有如下性质:
,使它同时具有如下性质: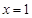 对称;②当x=2时,y>0;③当x=-2时,y<0.
对称;②当x=2时,y>0;③当x=-2时,y<0.