题目内容
20. 如图,在△ABC中,∠B=∠AED,AB=5,AD=3,CE=6,
如图,在△ABC中,∠B=∠AED,AB=5,AD=3,CE=6,求证:(1)△ADE∽△ABC;(2)求AE的长.
分析 (1)利用“两角法”进行证明;
(2)利用(1)中相似三角形的对应边成比例来求AE的长度.
解答 (1)证明:∵∠B=∠AED,∠A=∠A,
∴△ADE∽△ABC;
(2)解:由(1)知,△ADE∽△ABC,则$\frac{AD}{AB}$=$\frac{AE}{AC}$,即$\frac{AD}{AB}$=$\frac{AE}{AE+EC}$.
∵AB=5,AD=3,CE=6,
∴$\frac{3}{5}$=$\frac{AE}{AE+6}$,
∴AE=9.
点评 本题考查了相似三角形的判定与性质.本题关键是要懂得找相似三角形,利用相似三角形的性质求解.

练习册系列答案
相关题目
 如图,在⊙O中,AB为直径,C为⊙O上一点,∠A=40°,则∠B=50°.
如图,在⊙O中,AB为直径,C为⊙O上一点,∠A=40°,则∠B=50°.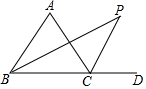 如图,△ABC的外角∠ACD的平分线:CP与内角∠ABC平分线BP交于点P,若∠A=60°,求∠P的度数.
如图,△ABC的外角∠ACD的平分线:CP与内角∠ABC平分线BP交于点P,若∠A=60°,求∠P的度数. 如图,已知四边形ABCD内接于⊙O,直径AC=6,对角线AC、BD交于E点,且AB=BD,EC=1,则AD的长是$\frac{3\sqrt{15}}{2}$.
如图,已知四边形ABCD内接于⊙O,直径AC=6,对角线AC、BD交于E点,且AB=BD,EC=1,则AD的长是$\frac{3\sqrt{15}}{2}$.