题目内容
15.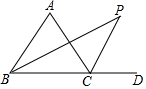 如图,△ABC的外角∠ACD的平分线:CP与内角∠ABC平分线BP交于点P,若∠A=60°,求∠P的度数.
如图,△ABC的外角∠ACD的平分线:CP与内角∠ABC平分线BP交于点P,若∠A=60°,求∠P的度数.
分析 根据角平分线的定义得到∠PCD=$\frac{1}{2}$∠ACD,∠PBC=$\frac{1}{2}$∠ABC,根据三角形的外角的性质计算即可.
解答 解:∵CP是∠ACD的平分线,
∴∠PCD=$\frac{1}{2}$∠ACD,
∵BP是∠ABC的平分线,
∴∠PBC=$\frac{1}{2}$∠ABC,
∴∠P=∠PCD-∠PBC=$\frac{1}{2}$×(∠ACD+∠ABC)=$\frac{1}{2}$∠A=30°.
点评 本题考查的是三角形的外角的性质、角平分线的性质,掌握三角形的一个外角等于和它不相邻的两个内角的和是解题的关键.

练习册系列答案
相关题目
6.下列各式中,一定成立的是( )
| A. | 22=(-2)2 | B. | -22=|-22| | C. | -(-2)3=-|-23| | D. | 23=(-23) |
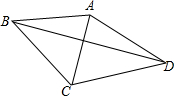 如图,线段AB=a,将线段AB绕点A逆时针旋转60°得到线段AC,继续旋转α(0°<α<120°)得到线段AD,连接BC,CD,BD.
如图,线段AB=a,将线段AB绕点A逆时针旋转60°得到线段AC,继续旋转α(0°<α<120°)得到线段AD,连接BC,CD,BD. 如图,在△ABC中,∠B=∠AED,AB=5,AD=3,CE=6,
如图,在△ABC中,∠B=∠AED,AB=5,AD=3,CE=6, ;
;  .
.