题目内容
14.在矩形ABCD中,P是边AB上一动点,PQ⊥DC交DC于Q,且分得两个新矩形相似,若AB=10,AD=4,则AP的长是2或8.分析 根据题意作出图形,利用相似矩形的对应边的比相等列出比例式代入数据求解即可.
解答  解:如图,当矩形APQD∽矩形PQCB时,
解:如图,当矩形APQD∽矩形PQCB时,
$\frac{AP}{PQ}$=$\frac{PQ}{PB}$,
即:$\frac{AP}{4}=\frac{4}{10-AP}$,
解得:AP=2或8,
故答案为:2或8.
点评 本题考查了相似多边形的性质,解题的关键是能够了解相似多边形的对应边的比相等,难度不大.

练习册系列答案
相关题目

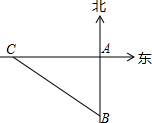 如图,一艘轮船以30km/h的速度沿既定航线由西向东航行,途中接到台风警报,某台风中心正以20km/h的途度由南向北移动,距台风中心200km的圆形区域(包括边界)都属台风影响区.当这艘轮船接到台风警报时,它与台风中心的距离BC=500km,此时台风中心与轮船既定航线的最近距离BA=300km.
如图,一艘轮船以30km/h的速度沿既定航线由西向东航行,途中接到台风警报,某台风中心正以20km/h的途度由南向北移动,距台风中心200km的圆形区域(包括边界)都属台风影响区.当这艘轮船接到台风警报时,它与台风中心的距离BC=500km,此时台风中心与轮船既定航线的最近距离BA=300km. 如图,在以O为圆心的两个同心圆中,AB经过圆心O,且与小圆相交于点A、与大圆相交于点B.小圆的切线AC与大圆相交于点D,且CO平分∠ACB.
如图,在以O为圆心的两个同心圆中,AB经过圆心O,且与小圆相交于点A、与大圆相交于点B.小圆的切线AC与大圆相交于点D,且CO平分∠ACB. 如图,在矩形ABCD中,已知AB=6cm,BC=8cm,连接BD,动点P从点B出发沿BD向终点D运动,速度为1厘米/秒,过点P作BD的垂线交折线BA-AD于点E,交折线BC-CD于点F,点P运动的时间为t(秒).
如图,在矩形ABCD中,已知AB=6cm,BC=8cm,连接BD,动点P从点B出发沿BD向终点D运动,速度为1厘米/秒,过点P作BD的垂线交折线BA-AD于点E,交折线BC-CD于点F,点P运动的时间为t(秒).