题目内容
13.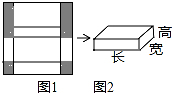 如图1是边长为18cm的正方形纸板,截掉阴影部分后将其折叠成如图2所示的长方体盒子.已知该长方体的宽是高的2倍,则它的体积是216cm3.
如图1是边长为18cm的正方形纸板,截掉阴影部分后将其折叠成如图2所示的长方体盒子.已知该长方体的宽是高的2倍,则它的体积是216cm3.
分析 设该长方体的高为x,则长方体的宽为2x,利用展开图得到2x+2x+x+x=18,然后解方程得到x的值,从而得到该长方体的高、宽、长,于是可计算出它的体积.
解答 解:设该长方体的高为x,则长方体的宽为2x,
2x+2x+x+x=18,解得x=3,
所以该长方体的高为3,则长方体的宽为6,长为18-6=12,
所以它的体积为3×6×12=216(cm2).
故答案为216.
点评 本题考查了展开图折叠成几何体:通过结合立体图形与平面图形的相互转化,去理解和掌握几何体的展开图,要注意多从实物出发,然后再从给定的图形中辨认它们能否折叠成给定的立体图形.

练习册系列答案
相关题目
1.某厂从2013年起开始投入资金改进技术,经技术改进后,某产品的生产成本不断降低,具体数据如下表:
(1)请你认真分析表中数据,从你所学习过的一次函数、二次函数和反比例函数中确定哪种函数能表示其变化规律?说明确定是这种函数而不是其他函数的理由,并求出它的解析式.
(2)按照这种变化规律,若2017年已投入技改资金5万元,预计生产成本每件比2016年降低多少万元?
| 年 度 | 2013 | 2014 | 2015 | 2016 |
| 投入技改资金x/万元) | 2.5 | 3 | 4 | 4.5 |
| 产品成本y(万元∕件) | 7.2 | 6 | 4.5 | 4 |
(2)按照这种变化规律,若2017年已投入技改资金5万元,预计生产成本每件比2016年降低多少万元?
18. 如图,在菱形ABCD中,对角线AC与BD相交于点O,OE⊥AB,垂足为E,若∠ADC=140°,则∠AOE的大小为( )
如图,在菱形ABCD中,对角线AC与BD相交于点O,OE⊥AB,垂足为E,若∠ADC=140°,则∠AOE的大小为( )
 如图,在菱形ABCD中,对角线AC与BD相交于点O,OE⊥AB,垂足为E,若∠ADC=140°,则∠AOE的大小为( )
如图,在菱形ABCD中,对角线AC与BD相交于点O,OE⊥AB,垂足为E,若∠ADC=140°,则∠AOE的大小为( )| A. | 70° | B. | 65° | C. | 55° | D. | 80° |
2.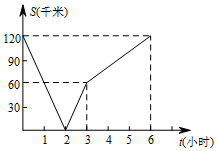 已知A,B两地相距120千米,甲乙两人沿同一条公路匀速行驶,甲骑自行车以20千米/时从A地前往B地,同时乙骑摩托车从B地前往A地,设两人之间的距离为s(千米),甲行驶的时间为t(小时),若s与t的函数关系如图所示,则下列说法错误的是( )
已知A,B两地相距120千米,甲乙两人沿同一条公路匀速行驶,甲骑自行车以20千米/时从A地前往B地,同时乙骑摩托车从B地前往A地,设两人之间的距离为s(千米),甲行驶的时间为t(小时),若s与t的函数关系如图所示,则下列说法错误的是( )
 已知A,B两地相距120千米,甲乙两人沿同一条公路匀速行驶,甲骑自行车以20千米/时从A地前往B地,同时乙骑摩托车从B地前往A地,设两人之间的距离为s(千米),甲行驶的时间为t(小时),若s与t的函数关系如图所示,则下列说法错误的是( )
已知A,B两地相距120千米,甲乙两人沿同一条公路匀速行驶,甲骑自行车以20千米/时从A地前往B地,同时乙骑摩托车从B地前往A地,设两人之间的距离为s(千米),甲行驶的时间为t(小时),若s与t的函数关系如图所示,则下列说法错误的是( )| A. | 经过2小时两人相遇 | |
| B. | 若乙行驶的路程是甲的2倍,则t=3 | |
| C. | 当乙到达终点时,甲离终点还有60千米 | |
| D. | 若两人相距90千米,则t=0.5或t=4.5 |
3.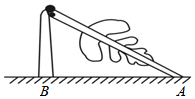 如图,一棵大树在一次强台风中距地面5m处折断,倒下后树顶端着地点A距树底端B的距离为12m,这棵大树在折断前的高度为( )
如图,一棵大树在一次强台风中距地面5m处折断,倒下后树顶端着地点A距树底端B的距离为12m,这棵大树在折断前的高度为( )
 如图,一棵大树在一次强台风中距地面5m处折断,倒下后树顶端着地点A距树底端B的距离为12m,这棵大树在折断前的高度为( )
如图,一棵大树在一次强台风中距地面5m处折断,倒下后树顶端着地点A距树底端B的距离为12m,这棵大树在折断前的高度为( )| A. | 10m | B. | 15m | C. | 18m | D. | 20m |
 有理数a,b在数轴上的位置如图所示,则-a>0,b>0,b-a>0,a+b>0.
有理数a,b在数轴上的位置如图所示,则-a>0,b>0,b-a>0,a+b>0.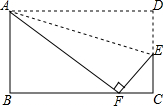 如图,小红将长方形ABCD沿AE折叠,顶点D恰好落在BC边上的F处,已知AB=8,BC=10,试求折痕AE的长.
如图,小红将长方形ABCD沿AE折叠,顶点D恰好落在BC边上的F处,已知AB=8,BC=10,试求折痕AE的长.