题目内容
19.从1、2、3、4四个整数中任取两个数作为一个点的坐标,那么这个点恰好在抛物线y=x2上的概率是( )| A. | $\frac{1}{24}$ | B. | $\frac{1}{12}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{4}$ |
分析 通过列表列出所有等可能结果,然后根据二次函数图象上点的坐标特征确定在函数图象上的点的情况数,再根据概率公式列式进行计算即可得解.
解答 解:列表如下:
| 1 | 2 | 3 | 4 | |
| 1 | (1,2) | (1,3) | (1,4) | |
| 2 | (2,1) | (2,3) | (2,4) | |
| 3 | (3,1) | (3,2) | (3,3) | |
| 4 | (4,1) | (4,2) | (4,3) |
其中点恰好在抛物线y=x2上的只有(2,4)这一个结果,
所以这个点恰好在抛物线y=x2上的概率是$\frac{1}{12}$,
故选:B.
点评 本题主要考查概率的计算,熟知:概率=所求情况数与总情况数之比以及二次函数图象上点的坐标特征是解题的根本.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
10.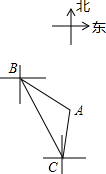 如图,轮船从B处以每小时60海里的速度沿南偏东20°方向匀速航行,在B处观测灯塔A位于南偏东50°方向上,轮船航行40分钟到达C处,在C处观测灯塔A位于北偏东10°方向上,求C处与灯塔A的距离.
如图,轮船从B处以每小时60海里的速度沿南偏东20°方向匀速航行,在B处观测灯塔A位于南偏东50°方向上,轮船航行40分钟到达C处,在C处观测灯塔A位于北偏东10°方向上,求C处与灯塔A的距离.
 如图,轮船从B处以每小时60海里的速度沿南偏东20°方向匀速航行,在B处观测灯塔A位于南偏东50°方向上,轮船航行40分钟到达C处,在C处观测灯塔A位于北偏东10°方向上,求C处与灯塔A的距离.
如图,轮船从B处以每小时60海里的速度沿南偏东20°方向匀速航行,在B处观测灯塔A位于南偏东50°方向上,轮船航行40分钟到达C处,在C处观测灯塔A位于北偏东10°方向上,求C处与灯塔A的距离.
7.下列图形中,既是轴对称又是中心对称图形的是( )
| A. | 正五边形 | B. | 等腰梯形 | C. | 平行四边形 | D. | 圆 |