题目内容
把下列各式分解因式
(1)8x3-8x2-4x;
(2)6x3y(x-y)3-4xy3(y-x)2;
(3)15x(a-b)2-3y(b-a);
(4)(2x+y)2-(x-2y)2.
(1)8x3-8x2-4x;
(2)6x3y(x-y)3-4xy3(y-x)2;
(3)15x(a-b)2-3y(b-a);
(4)(2x+y)2-(x-2y)2.
考点:提公因式法与公式法的综合运用
专题:
分析:(1)先提取公因式8x,再根据公式法进行二次分解;
(2)提取公因式2xy(x-y)2,再化简即可求解;
(3)提取公因式(a-b),再化简即可求解;
(4)利用平方差公式分解因式,再化简即可求解.
(2)提取公因式2xy(x-y)2,再化简即可求解;
(3)提取公因式(a-b),再化简即可求解;
(4)利用平方差公式分解因式,再化简即可求解.
解答:解:(1)8x3-8x2-4x
=8x(x2-x-
)
=8x(x-
)(x-
);
(2)6x3y(x-y)3-4xy3(y-x)2
=2xy(x-y)2[3x2(x-y)-2y]
=2xy(x-y)2(3x3-3x2y-2y);
(3)15x(a-b)2-3y(b-a);
=15x(a-b)2+3y(a-b)
=3(a-b)(5a-5b+y);
(4)(2x+y)2-(x-2y)2
=[(2x+y)+(x-2y)][(2x+y)-(x-2y)]
=(3x-y)(x+3y).
=8x(x2-x-
| 1 |
| 2 |
=8x(x-
1+
| ||
| 2 |
1-
| ||
| 2 |
(2)6x3y(x-y)3-4xy3(y-x)2
=2xy(x-y)2[3x2(x-y)-2y]
=2xy(x-y)2(3x3-3x2y-2y);
(3)15x(a-b)2-3y(b-a);
=15x(a-b)2+3y(a-b)
=3(a-b)(5a-5b+y);
(4)(2x+y)2-(x-2y)2
=[(2x+y)+(x-2y)][(2x+y)-(x-2y)]
=(3x-y)(x+3y).
点评:本题考查了用提公因式法和公式法进行因式分解,一个多项式有公因式首先提取公因式,然后再用其他方法进行因式分解,同时因式分解要彻底,直到不能分解为止.

练习册系列答案
相关题目
已知开口向上的抛物线y=ax2+bx+c经过点(4,-6)、(-2,0),与x轴交于点A、B两点,与y轴交于点C,则△ABC面积的最小值是( )
A、10+4
| ||
B、10-4
| ||
C、10+4
| ||
D、10-4
|




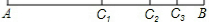 如图,线段AB的长为1,C1为AB的中点;C2为C1B的中点;…Cn为Cn-1的中点(n是大于1的正整数),观察思考:AC1=
如图,线段AB的长为1,C1为AB的中点;C2为C1B的中点;…Cn为Cn-1的中点(n是大于1的正整数),观察思考:AC1=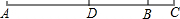 如图,延长线段AB到点C,使BC=
如图,延长线段AB到点C,使BC=