Question

已知开口向上的抛物线y=ax²+bx+c经过点（4，-6）、（-2，0），与x轴交于点A、B两点，与y轴交于点C，则△ABC面积的最小值是（　　）

• A、10+4

  5

• B、10-4

  5

• C、10+4

  6

• D、10-4

  6

Answer 1

考点：抛物线与x轴的交点

专题：

分析：将点（4，-6）（-2，0）分别代入抛物线方程推知c=-2a-8．设点B的横坐标是m，则-2和m是方程ax²+bx+c=0的两根，则利用根与系数的关系得到-2m=

c

a

，故m=-

c

2a

．最后利用三角形的面积公式和不等式的性质进行解答．

解答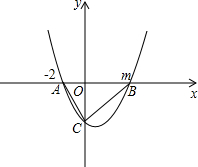：解：把（4，-6）、（-2，0）分别代入y=ax²+bx+c，得
16a+4b+c=-6①，
4a-2b+c=0②，
由①②，得
c=-2a-8．③
设B（m，0），
则-2m=

c

a

，故m=-

c

2a

．
所以S_△ABC=

1

2

|c|•|m+2|
=-

1

2

c（-

c

2a

+2）
=

c2-4ac

4a

=

(-2a+8)2-4a(-2a-8)

4a

=10+24a+

1

a

．
∵24a+

1

a

≥2

24a× 1 a

=4

6

，
∴10+24a+

1

a

≥10+4

6

．
即△ABC面积的最小值是10+4

6

．
故选：C．

点评：本题考查了抛物线与x轴的交点．在解题过程中，利用已知条件推知a、c间的数量关系是解题的关键．