题目内容
20.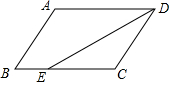 如图,在?ABCD中,DE平分∠ADC,AD=9,BE=3,则?ABCD的周长是30.
如图,在?ABCD中,DE平分∠ADC,AD=9,BE=3,则?ABCD的周长是30.
分析 首先由在?ABCD中,AD=9,BE=3,求得CE的长,然后由DE平分∠ADC,证得△CED是等腰三角形,继而求得CD的长,则可求得答案.
解答 解:∵在?ABCD中,AD=9,
∴BC=AD=9,AD∥BC,
∴CE=BC-BE=9-3=6,∠ADE=∠CED,
∵DE平分∠ADC,
∴∠ADE=∠CDE,
∴∠CDE=∠CED,
∴CD=CE=6,
∴?ABCD的周长是:2(AD+CD)=30.
故答案为:30.
点评 此题考查了平行四边形的性质以及等腰三角形的判定与性质.注意证得△CED是等腰三角形是解此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.下列运算正确的是( )
| A. | (-2xy)(-3xy)3=-54x4y4 | B. | 5a2•(3a3)2=15a12 | ||
| C. | (-0.1x)(-10x2)3=-x2 | D. | (2×10n)(0.5×10n)=102n |
5.下列方程组中哪一个是二元一次方程组( )
| A. | $\left\{\begin{array}{l}{m-n=1}\\{m+n=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{y-z=0}\\{x+y=1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+y=1}\\{xy=-2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=1}\\{\frac{1}{x}-\frac{1}{y}=32}\end{array}\right.$ |
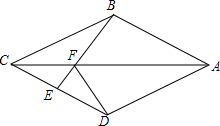 如图,在四边形ABCD中,AB=AD、CB=CD,E是CD上一点,BE交AC于F,连接DF.
如图,在四边形ABCD中,AB=AD、CB=CD,E是CD上一点,BE交AC于F,连接DF.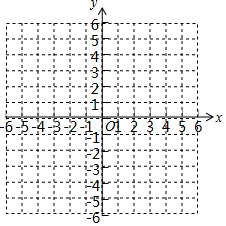 已知:A(0,1),B(2,0),C(4,3)
已知:A(0,1),B(2,0),C(4,3)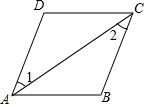 如图,完成下列推理,并填写理由,如图,∠B=∠D,∠1=∠2,求证:AB∥CD.
如图,完成下列推理,并填写理由,如图,∠B=∠D,∠1=∠2,求证:AB∥CD.