题目内容
8. 如图,一天我国一渔政船航行到A处时,发现在南偏东60°方向,相距20海里的P处有一可疑渔船,正沿西南方向向我领海区域航行,我渔政船立即沿正南方向航行拦截,2小时后,在我领海区域的B处截获可疑渔船.请求出我渔政船从A处航行到B处的航程(结果保留根号).
如图,一天我国一渔政船航行到A处时,发现在南偏东60°方向,相距20海里的P处有一可疑渔船,正沿西南方向向我领海区域航行,我渔政船立即沿正南方向航行拦截,2小时后,在我领海区域的B处截获可疑渔船.请求出我渔政船从A处航行到B处的航程(结果保留根号).
分析 作PE⊥AB于点E,首先在Rt△APE中求得AE的长,然后在Rt△BPE中求得BE的长,再根据AB=AE+BE计算即可.
解答  解:作PE⊥AB于点E,
解:作PE⊥AB于点E,
在Rt△APE中,∵∠AEP=90°,∠PAE=60°,AP=20海里,
∴∠APE=30°,
∴AE=$\frac{1}{2}$AP=10海里,PE=$\sqrt{3}$AE=10$\sqrt{3}$海里.
在Rt△BPE中,∵∠BEP=90°,∠BPE=45°,
∴BE=PE=10$\sqrt{3}$海里,
∴AB=AE+BE=10+10$\sqrt{3}$(海里).
答:我渔政船从A处航行到B处的航程为(10+10$\sqrt{3}$)海里.
点评 本题考查了解直角三角形的应用-方向角问题,解题的关键是从实际问题中构造出直角三角形并利用直角三角形的性质求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18. 随县炎帝神农大像底座边长56尺,意为中国56个民族,底座高度为42.6尺,意为炎帝神农诞生日农历四月二十六日;立像高为95尺(约34.670米),唐县镇七年级同学张婉秋在参观后问:“31.670米这个数有几个有效数字,精确到哪一位呢?”( )
随县炎帝神农大像底座边长56尺,意为中国56个民族,底座高度为42.6尺,意为炎帝神农诞生日农历四月二十六日;立像高为95尺(约34.670米),唐县镇七年级同学张婉秋在参观后问:“31.670米这个数有几个有效数字,精确到哪一位呢?”( )
 随县炎帝神农大像底座边长56尺,意为中国56个民族,底座高度为42.6尺,意为炎帝神农诞生日农历四月二十六日;立像高为95尺(约34.670米),唐县镇七年级同学张婉秋在参观后问:“31.670米这个数有几个有效数字,精确到哪一位呢?”( )
随县炎帝神农大像底座边长56尺,意为中国56个民族,底座高度为42.6尺,意为炎帝神农诞生日农历四月二十六日;立像高为95尺(约34.670米),唐县镇七年级同学张婉秋在参观后问:“31.670米这个数有几个有效数字,精确到哪一位呢?”( )| A. | 有4个有效数字,精确到千分位 | B. | 有3个有效数字,精确到万分位 | ||
| C. | 有5个有效数字,精确到千分位 | D. | 有3个有效数字,精确到十位 |
16.已知点P关于x轴的对称点P′的坐标为(-1,5),则点P的坐标是( )
| A. | (1,5) | B. | (-1,-5) | C. | (5,1) | D. | (-5,-1) |
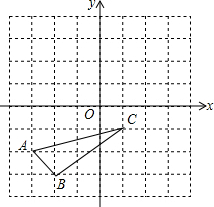 如图,△ABC是格点三角形,且A(-3,-2),B(-2,-3),C(1,-1)
如图,△ABC是格点三角形,且A(-3,-2),B(-2,-3),C(1,-1) 已知,⊙O与正六边形0ABCDE的边0A、0E分别交于点F、G,则弧FG所对的圆周角∠FPG的正弦值为$\frac{\sqrt{3}}{2}$.
已知,⊙O与正六边形0ABCDE的边0A、0E分别交于点F、G,则弧FG所对的圆周角∠FPG的正弦值为$\frac{\sqrt{3}}{2}$.