题目内容
4.下列计算正确的是( )| A. | $\sqrt{12}$=2$\sqrt{3}$ | B. | $\sqrt{\frac{3}{2}}$=$\frac{\sqrt{3}}{2}$ | C. | $\sqrt{-{x}^{3}}$=x$\sqrt{-x}$ | D. | $\sqrt{{x}^{2}}$=x |
分析 直接利用二次根式的性质分别化简求出答案.
解答 解:A、$\sqrt{12}$=2$\sqrt{3}$,正确;
B、$\sqrt{\frac{3}{2}}$=$\frac{\sqrt{6}}{2}$,故此选项错误;
C、$\sqrt{-{x}^{3}}$=-x$\sqrt{-x}$,故此选项错误;
D、$\sqrt{{x}^{2}}$=|x|,故此选项错误;
故选:A.
点评 此题主要考查了二次根式的化简,正确掌握二次根式的性质是解题关键.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
14.已知等边三角形的边长为3,点P为等边三角形内任意一点,则点P到三边的距离之和为( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{3\sqrt{3}}{2}$ | C. | $\frac{3}{2}$ | D. | 不能确定 |
15. 如图,一个放置在水平桌面上的圆柱,它的主(正)视图是( )
如图,一个放置在水平桌面上的圆柱,它的主(正)视图是( )
 如图,一个放置在水平桌面上的圆柱,它的主(正)视图是( )
如图,一个放置在水平桌面上的圆柱,它的主(正)视图是( )| A. |  | B. |  | C. |  | D. |  |
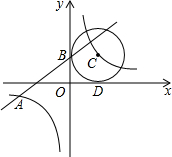 如图,已知一次函数y1=kx+b的图象与反比例函数y2=$\frac{4}{x}$的图象交于点A(-4,m),且与y轴交于点B,第一象限内点C在反比例函数y2=$\frac{4}{x}$的图象上,且以点C为圆心的圆与x轴,y轴分别相切于点D,B
如图,已知一次函数y1=kx+b的图象与反比例函数y2=$\frac{4}{x}$的图象交于点A(-4,m),且与y轴交于点B,第一象限内点C在反比例函数y2=$\frac{4}{x}$的图象上,且以点C为圆心的圆与x轴,y轴分别相切于点D,B 如图,在Rt△ABC中,∠ACB=90°,∠BAC的平分线交BC于点O,OC=1,以点O为圆心OC为半径作半圆.
如图,在Rt△ABC中,∠ACB=90°,∠BAC的平分线交BC于点O,OC=1,以点O为圆心OC为半径作半圆. 已知不等式组$\left\{\begin{array}{l}{x≥-a-1}&{①}\\{-x≥-b}&{②}\end{array}\right.$,在同一条数轴上表示不等式①,②的解集如图所示,则b-a的值为$\frac{1}{3}$.
已知不等式组$\left\{\begin{array}{l}{x≥-a-1}&{①}\\{-x≥-b}&{②}\end{array}\right.$,在同一条数轴上表示不等式①,②的解集如图所示,则b-a的值为$\frac{1}{3}$.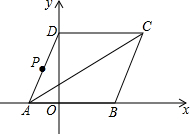 如图所示,菱形ABCD的顶点A、B在x轴上,点A在点B的左侧,点D在y轴的正半轴上,∠BAD=60°.点A的坐标为(-2,0).
如图所示,菱形ABCD的顶点A、B在x轴上,点A在点B的左侧,点D在y轴的正半轴上,∠BAD=60°.点A的坐标为(-2,0).