题目内容
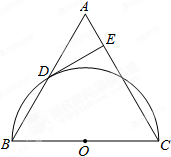 已知:如图,在△ABC中,AB=AC,以BC为直径的半圆O与边AB相交于点D,切线DE⊥AC,垂足为点E.求证:
已知:如图,在△ABC中,AB=AC,以BC为直径的半圆O与边AB相交于点D,切线DE⊥AC,垂足为点E.求证:(1)△ABC是等边三角形;
(2)AE=
| 1 |
| 4 |
考点:切线的性质
专题:证明题
分析:(1)连结OD,如图,根据切线的性质得OD⊥DE,易得OD∥AC,则∠DOB=∠C,由于∠B=∠C,则∠B=∠DOB,接着证明△DBO为等边三角形,得到∠B=60°,然后根据等边三角形的判定方法即可得到△ABC是等边三角形;
(2)由于△ABC是等边三角形,则∠A=60°,根据含30度的直角三角形三边的关系得到AE=
AD,再证明D点为AB的中点,即AD=BD,则AE=
AB,于是有AE=
AC.
(2)由于△ABC是等边三角形,则∠A=60°,根据含30度的直角三角形三边的关系得到AE=
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
解答:证明: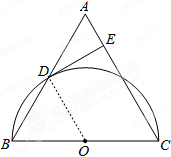 (1)连结OD,如图,
(1)连结OD,如图,
∵以BC为直径的半圆O与边AB相交于点D,
∴OD⊥DE,
∵DE⊥AC,
∴OD∥AC,
∴∠DOB=∠C,
∵AB=AC,
∴∠B=∠C,
∴∠B=∠DOB,
∴DB=DO,
∴DB=DO=BO,
∴△DBO为等边三角形,
∴∠B=60°,
而AB=AC,
∴△ABC是等边三角形;
(2)∵△ABC是等边三角形,
∴∠A=60°,
∴∠ADE=30°,
∴AE=
AD,
∵OD∥AC,点O为BC的中点,
∴D点为AB的中点,即AD=BD,
∴AE=
AB,
∴AE=
AC.
 (1)连结OD,如图,
(1)连结OD,如图,∵以BC为直径的半圆O与边AB相交于点D,
∴OD⊥DE,
∵DE⊥AC,
∴OD∥AC,
∴∠DOB=∠C,
∵AB=AC,
∴∠B=∠C,
∴∠B=∠DOB,
∴DB=DO,
∴DB=DO=BO,
∴△DBO为等边三角形,
∴∠B=60°,
而AB=AC,
∴△ABC是等边三角形;
(2)∵△ABC是等边三角形,
∴∠A=60°,
∴∠ADE=30°,
∴AE=
| 1 |
| 2 |
∵OD∥AC,点O为BC的中点,
∴D点为AB的中点,即AD=BD,
∴AE=
| 1 |
| 4 |
∴AE=
| 1 |
| 4 |
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,得到垂直关系,构造直角三角形.

练习册系列答案
相关题目
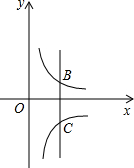 如图,直线x=t(t>0)与反比例函数y=
如图,直线x=t(t>0)与反比例函数y=| 2 |
| x |
| 3 |
| x |
| A、5 | ||
B、
| ||
C、
| ||
| D、不能确定 |
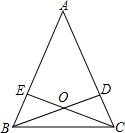 如图,已知AB=AC,AE=AD,则①△ABD≌△ACE,②△BOE≌△COD,③点O在∠BAC的平分线上,( )
如图,已知AB=AC,AE=AD,则①△ABD≌△ACE,②△BOE≌△COD,③点O在∠BAC的平分线上,( )| A、都正确 |
| B、都不正确 |
| C、只有一个正确 |
| D、只有一个不正确 |
在Rt△ABC中,∠C=90°,斜边c=3,那么直角边a、b有关系式( )
| A、a+b=3 |
| B、a2+b2=3 |
| C、a2+b2=9 |
| D、ab=3 |
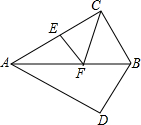 两个全等的含30°的直角三角板如图放置(斜边重合),点E是AC的中点,AC=2,若点F是直线AB上的一个动点,则△CEF的周长最小值是
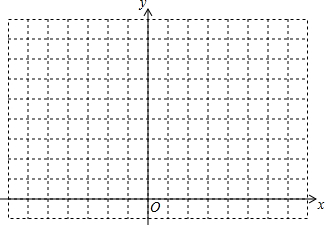
两个全等的含30°的直角三角板如图放置(斜边重合),点E是AC的中点,AC=2,若点F是直线AB上的一个动点,则△CEF的周长最小值是 如图,在正方形网格中,△ABC各顶点都在格点上,点A,C的坐标分别为(-5,1)、(-1,4),结合所给的平面直角坐标系解答下列问题:
如图,在正方形网格中,△ABC各顶点都在格点上,点A,C的坐标分别为(-5,1)、(-1,4),结合所给的平面直角坐标系解答下列问题: 如图,将一副三角板叠放在一起,其中AB=14cm,∠B=30°,∠D=45°,求△ACF的面积.
如图,将一副三角板叠放在一起,其中AB=14cm,∠B=30°,∠D=45°,求△ACF的面积.