题目内容
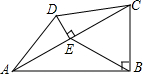 如图,在四边形ABCD中,∠ABC=90°,∠CAB=30°,DE⊥AC于E,且AE=CE,若DE=5,EB=12.求四边形ABCD的面积和∠DAC的正弦值.
如图,在四边形ABCD中,∠ABC=90°,∠CAB=30°,DE⊥AC于E,且AE=CE,若DE=5,EB=12.求四边形ABCD的面积和∠DAC的正弦值.考点:面积及等积变换
专题:
分析:由∠ABC=90°,AE=CE,EB=12,根据直角三角形斜边的中线等于斜边的一半,即可求得AC的长,又由∠CAB=30°,利用三角函数的知识即可求得BC与AB的长,然后由S四边形ABCD=S△ABC+S△ACD,求得四边形ABCD的面积;利用勾股定理即可求得AD的长,继而求得∠DAC的正弦值.
解答:解:∵∠ABC=90°,AE=CE,EB=12,
∴AC=2BE=24.
∵在Rt△ABC中,∠CAB=30°,
∴BC=
AC=12,AB=AC•cos30°=12
,
∵DE⊥AC,DE=5,
∴S四边形ABCD=S△ABC+S△ACD=
AB•BC+
AC•DE=72
+60,
在Rt△ADE中,AD=
=
=13,
∴sin∠DAC=
=
.
∴AC=2BE=24.
∵在Rt△ABC中,∠CAB=30°,
∴BC=
| 1 |
| 2 |
| 3 |
∵DE⊥AC,DE=5,
∴S四边形ABCD=S△ABC+S△ACD=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
在Rt△ADE中,AD=
| AE2+DE2 |
| 122+52 |
∴sin∠DAC=
| DE |
| AD |
| 5 |
| 13 |
点评:此题考查了面积与等积变换的知识.注意应用直角三角形的性质、三角函数以及勾股定理.此题难度适中,注意把四边形分成两个三角形求解是解此题的关键.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
使
÷
有意义的x的值是( )
| x+3 |
| x-3 |
| x+2 |
| x-4 |
| A、x≠3且x≠4 |
| B、x≠-3且x≠4 |
| C、x≠3且x≠-2且x≠4 |
| D、x≠-3且x≠3且x≠-2且x≠4 |
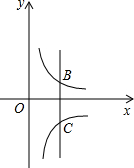 如图,直线x=t(t>0)与反比例函数y=
如图,直线x=t(t>0)与反比例函数y=| 2 |
| x |
| 3 |
| x |
| A、5 | ||
B、
| ||
C、
| ||
| D、不能确定 |
 如图,在△ABC中,DE是中位线,若∠ADE=60°,BC=8cm,则∠B=
如图,在△ABC中,DE是中位线,若∠ADE=60°,BC=8cm,则∠B=