题目内容
9.用min{a、b、c}表示这三个数中最小的数,则min{sin30°、cos45°、tan30°}=sin30°.分析 先根据特殊角的三角函数值求出sin30°、cos45°、tan30°的值,再比较其大小即可.
解答 解:sin30°=$\frac{1}{2}$,cos45°=$\frac{\sqrt{2}}{2}$,tan30°=$\frac{\sqrt{3}}{3}$,
∵$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7,
∴$\frac{\sqrt{2}}{2}$≈0.7,$\frac{\sqrt{3}}{3}$≈0.54.
∵0.7>0.54>0.5,
∴$\frac{\sqrt{2}}{2}$>$\frac{\sqrt{3}}{3}$>$\frac{1}{2}$,即cos45°>tan30°>sin30°,
∴min{sin30°、cos45°、tan30°}=sin30°.
故答案为:sin30°.
点评 本题考查的是特殊角的三角函数值,熟记各特殊角度的三角函数值是解答此题的关键.

练习册系列答案
相关题目
20. 如图,把△ABC绕点C逆时针旋转90°得到△DCE,若∠A=35°,则∠ADE为( )
如图,把△ABC绕点C逆时针旋转90°得到△DCE,若∠A=35°,则∠ADE为( )
 如图,把△ABC绕点C逆时针旋转90°得到△DCE,若∠A=35°,则∠ADE为( )
如图,把△ABC绕点C逆时针旋转90°得到△DCE,若∠A=35°,则∠ADE为( )| A. | 35° | B. | 55° | C. | 135° | D. | 125° |
4. 如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下一次沿顺时针方向跳两个点;若停在偶数点上,则下一次沿逆时针方向跳一个点.若青蛙从5这点开始跳,则经2013次跳后它停在的点所对应的数为( )
如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下一次沿顺时针方向跳两个点;若停在偶数点上,则下一次沿逆时针方向跳一个点.若青蛙从5这点开始跳,则经2013次跳后它停在的点所对应的数为( )
 如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下一次沿顺时针方向跳两个点;若停在偶数点上,则下一次沿逆时针方向跳一个点.若青蛙从5这点开始跳,则经2013次跳后它停在的点所对应的数为( )
如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下一次沿顺时针方向跳两个点;若停在偶数点上,则下一次沿逆时针方向跳一个点.若青蛙从5这点开始跳,则经2013次跳后它停在的点所对应的数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 5 |
14.四边形ABCD的对角线相交于O,且AO=BO=CO=DO,则这个四边形( )
| A. | 仅是轴对称图形 | |
| B. | 仅是中心对称图形 | |
| C. | 既是轴对称图形又是中心对称图形 | |
| D. | 既不是轴对称图形,又不是中心对称图形 |
1.若多项式乘法(x+2y)(2x-ky-1)的结果中不含xy项,则k的值为( )
| A. | 4 | B. | -4 | C. | 2 | D. | -2 |
19.A为数轴上表示-1的点,将A点沿数轴向左移动2个单位长度到B点,则B点所表示的数为( )
| A. | 1或-3 | B. | 3 | C. | 1 | D. | -3 |
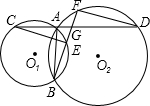 如图:已知⊙O1和⊙O2相交于A、B两点,过A的直线交两圆于C、D两点,过B 的直线交两圆于E、F两点,CD与EF交于点G,连接DF、CE.G为CD的中点.求证:CE=DF.
如图:已知⊙O1和⊙O2相交于A、B两点,过A的直线交两圆于C、D两点,过B 的直线交两圆于E、F两点,CD与EF交于点G,连接DF、CE.G为CD的中点.求证:CE=DF.