Question

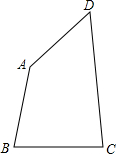如图，在凸四边形ABCD中，C、D为定点，CD=3，A、B为动点，满足AB=BC=DA=1．
（Ⅰ）写出cosC与cosA的关系式；
（Ⅱ）设△BCD和△ABD的面积分别为S和T，求S²+T²的最大值．

Answer 1

考点：正弦定理与余弦定理

专题：

分析：（Ⅰ）连结BD，在△BCD中及在△ABD中，利用余弦定理分别表示BD²，BD²=BD²的相等关系即可得出cosC与cosA的关系式；
（Ⅱ）利用正弦定理表示出S及T，利用（Ⅰ）的关系式表示出S²+T²即可得出S²+T²的最大值．

解答：解：（Ⅰ）如图，连结BD，

∵CD=3，AB=BC=DA=1．
∴在△BCD中，利用余弦定理得：BD²=BC²+CD²-2BC•CDcosC=10-6cosC
在△ABD中，BD²=2-2cosA，
∴10-6cosC=2-2cosA，
∴cosA=3cosC-4，
（Ⅱ）S=

1

2

BC•CD•sinC=

3

2

sinC，T=

1

2

AB•ADsinA=

1

2

sinA，
∵cosA=3cosC-4，
∴S²+T²=

9

4

sin²C+

1

4

sin²A=

9

4

（1-cos²C）+

1

4

（1-cos²A）=

5

2

-

9

4

cos²C-

1

4

cos²A=-

9

2

cos²C+6cosC-

3

2

=-(

3 2

2

cosC-

2

)2+

1

2

，
∴当cosC=

2

3

时，S²+T²的最大值是

1

2

．

点评：本题主要考查了正弦定理与余弦定理及三角形面积公式，熟练掌握正弦定理与余弦定理是解题的关键．