题目内容
15.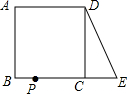 如图,在正方形ABCD中,AB=2,延长BC到点E,使CE=1,连接DE,动点P从点A出发以每秒1个单位的速度沿AB-BC-CD-DA向终点A运动,设点P的运动时间为t秒,当△ABP和△DCE全等时,t的值为( )
如图,在正方形ABCD中,AB=2,延长BC到点E,使CE=1,连接DE,动点P从点A出发以每秒1个单位的速度沿AB-BC-CD-DA向终点A运动,设点P的运动时间为t秒,当△ABP和△DCE全等时,t的值为( )| A. | 3 | B. | 5 | C. | 7 | D. | 3或7 |
分析 分两种情况进行讨论,根据题意得出BP=t-2=1和AP=8-t=1即可求得.
解答 解:因为在△ABP与△DCE中,
$\left\{\begin{array}{l}{AB=CD}\\{∠ABP=∠DCE=90°}\\{BP=CE}\end{array}\right.$,
∴△ABP≌△DCE,
由题意得:BP=t-2=1,
所以t=3,
因为在△ABP与△DCE中,
$\left\{\begin{array}{l}{AB=DC}\\{∠BAP=∠DCE=90°}\\{AP=CE}\end{array}\right.$,
∴△ABP≌△DCE,
由题意得:AP=8-t=1,
解得t=7.
所以,当t的值为3或7秒时.△ABP和△DCE全等.
故选D
点评 本题考查了全等三角形的判定,关键是根据三角形全等的判定方法有:ASA,SAS,AAS,SSS,HL解答.

练习册系列答案
相关题目
6.已知△ABC中,求作一点P,使P到∠A的两边的距离相等,且PB=PC,则下列确定P点的方法正确的是( )
| A. | P是∠A与∠B两角平分线的交点 | |
| B. | P是AC、AB两边上中垂线的交点 | |
| C. | P是∠A的角平分线与BC的中垂线的交点 | |
| D. | P是∠A的角平分线与AB的中垂线的交点 |
10.当a>0时,下列关于幂的运算正确的是( )
| A. | a-1=-a | B. | a0=1 | C. | (-a)2=-a2 | D. | (-ab)3=-ab3 |
20.如果把分式$\frac{5xy}{x+y}$的x与y都扩大10倍,那么这个分式的值( )
| A. | 不变 | B. | 扩大50倍 | C. | 扩大10 | D. | 缩小50倍 |
5. 如图,直线l1∥l2,若∠1=50°,则∠2的度数是( )
如图,直线l1∥l2,若∠1=50°,则∠2的度数是( )
 如图,直线l1∥l2,若∠1=50°,则∠2的度数是( )
如图,直线l1∥l2,若∠1=50°,则∠2的度数是( )| A. | 40° | B. | 50° | C. | 90° | D. | 130° |
 利用尺规、用三种不同的方法作一个三角形与已知直角三角形ABC全等,并简要说明理由.(同种理由视为是同一种方法)
利用尺规、用三种不同的方法作一个三角形与已知直角三角形ABC全等,并简要说明理由.(同种理由视为是同一种方法)