题目内容
6. 如图,直线L1∥L2,圆O与L1和L2分别相切于点A和点B,点M和点N分别是L1和L2上的动点,MN沿L1和L2平移,圆O的半径为1,∠1=60°,当MN与圆相切时,AM的长度等于$\sqrt{3}$或$\frac{\sqrt{3}}{3}$.
如图,直线L1∥L2,圆O与L1和L2分别相切于点A和点B,点M和点N分别是L1和L2上的动点,MN沿L1和L2平移,圆O的半径为1,∠1=60°,当MN与圆相切时,AM的长度等于$\sqrt{3}$或$\frac{\sqrt{3}}{3}$.
分析 当MN在左侧与⊙O相切时,连接OM、OA,则OM平分∠1,在Rt△OAM中可求得AM;当MN在右侧与⊙O相切时,连接OM、OA,则OM平分∠AMN,在Rt△OAM中可求得MA的长,可求得答案.
解答 解:
当MN在左侧与⊙O相切时,连接OM、OA,如图1,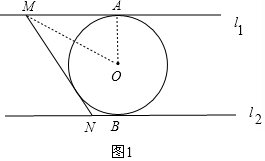
∵MA、MN是⊙O的切线,
∴OM平分∠AMN,OA⊥MA,
∴∠AMO=30°,
∴OM=2OA=2,
在Rt△OAM中,MA=$\sqrt{O{M}^{2}-O{A}^{2}}$=$\sqrt{3}$;
当MN在右侧与⊙O相切时,连接OM、OA,如图2,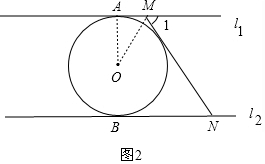
∵∠1=60°,
∴∠AMN=120°,
同上可知∠AMO=$\frac{1}{2}$∠AMN=60°,
∴OM=2AM,
在Rt△OAM中,MA2=OM2-OA2,即MA2=4MA2-1,解得MA=$\frac{\sqrt{3}}{3}$;
综上可知MA的长度为$\sqrt{3}$或$\frac{\sqrt{3}}{3}$,
故答案为:$\sqrt{3}$或$\frac{\sqrt{3}}{3}$.
点评 本题主要考查切线的性质,构造直角三角形,利用勾股定理求线段长度是解题的关键,注意分两种情况讨论.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
14.下列各数中,为负数的是( )
| A. | -1 | B. | 0 | C. | 2 | D. | 3.14 |
11.下列二次函数的图象中,开口最大的是( )
| A. | y=x2 | B. | y=2x2 | C. | y=$\frac{1}{100}$x2 | D. | y=-x2 |
18.在数2,$\frac{π}{3}$,-3.14,$\frac{22}{7}$,0.$\stackrel{•}{2}\stackrel{•}{3}$,5.1010010001中,无理数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
15. 如图,CD⊥AB,BE⊥AC,垂足分别为点D,点E,BE、CD相交于点O.∠1=∠2,则图中全等三角形共有( )
如图,CD⊥AB,BE⊥AC,垂足分别为点D,点E,BE、CD相交于点O.∠1=∠2,则图中全等三角形共有( )
 如图,CD⊥AB,BE⊥AC,垂足分别为点D,点E,BE、CD相交于点O.∠1=∠2,则图中全等三角形共有( )
如图,CD⊥AB,BE⊥AC,垂足分别为点D,点E,BE、CD相交于点O.∠1=∠2,则图中全等三角形共有( )| A. | 2对 | B. | 3对 | C. | 4对 | D. | 5对 |
 ,侧面展开图是半圆,则圆锥的侧面积是_________
,侧面展开图是半圆,则圆锥的侧面积是_________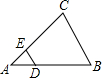 如图,在△ABC中,DE∥BC,DB=2AD,△ADE的面积为1,则四边形DBCE的面积为( )
如图,在△ABC中,DE∥BC,DB=2AD,△ADE的面积为1,则四边形DBCE的面积为( )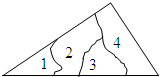 如图,一块三角形玻璃碎成了4块,现在要到玻璃店去配一块与原来的三角形玻璃完全一样的玻璃,那么最省事的办法是带( )去.
如图,一块三角形玻璃碎成了4块,现在要到玻璃店去配一块与原来的三角形玻璃完全一样的玻璃,那么最省事的办法是带( )去.