题目内容

18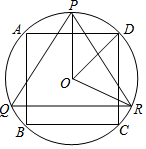．如图，△PQR是⊙O的内接正三角形，四边形ABCD是⊙O的内接正方形，BC∥QR，则∠DOR的度数是（　　）
A．60B．65C．72D．75

分析 根据等边三角形和正方形的性质，求得中心角∠POR和∠POD，二者的差就是所求．

解答 解：连结OA，如图，
∵△PQR是⊙O的内接正三角形，
∴PQ=PR=QR，
∴∠POR=$\frac{1}{3}$×360°=120°，
∵四边形ABCD是⊙O的内接正方形，
∴∠AOD=90°，
∴∠DOP=$\frac{1}{2}$×90°=45°，
∴∠DOR=∠POR-∠DOP=75°．
故选D．

点评 本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．也考查了垂径定理．

练习册系列答案
相关题目
15．下列计算错的是（　　）
A．a•a3•a4=a8B．a4•a3•（-a）=a7C．（a2）3=a6D．a5+a5=2a5
9．从多边形一条边上的一点（不是顶点）出发，连接各个顶点得到2013个三角形，则这个多边形的边数为（　　）
A．2011B．2015C．2014D．2016
6．在△ABC中，∠A，∠B，∠C的对应边分别为a，b，c，若∠A+∠C=90°，则（　　）
A．a2+b2=c2B．a2+c2=b2C．b2+c2=a2D．a=c
13．李明同学在电脑中设计了一个有理数的运算程序：输入“a”和“*”，再输入“b”，就可以得到运算：a*b=（a-2b）÷（2a-b）．
（1）试求（-3）*$\frac{1}{3}$的值；
（2）王华在运用这个程序计算3*6时，屏幕上显示：“该操作无法进行．”请你说明操作无法进行的原因．
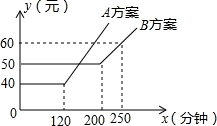3．如图，某电信公司提供了一个月使用移动通讯工具的A，B两种方案的通讯费用y（元）与通话时间x（元）之间的关系，下面给出了关于A、B两种方案的看法：
①若通话时间少于120分钟，则A方案比B方案始终便宜10元；
②两种通话方案永远不可能在某一通话时刻费用相同；
③在通话时间超过200分钟时，A方案的费用始终高于B方案费用．
则以上说法正确的是（　　）
A．①②B．①③C．②③D．①②③
10．方程x2=x的解是（　　）
A．x=1B．x=0C．x1=1   x2=0D．x1=-1   x2=0
7．（1）（-5）+2$\frac{2}{3}$+（-$\frac{1}{2}$）+（-2$\frac{2}{3}$）
（2）（-$\frac{1}{2}$+$\frac{2}{3}$-$\frac{1}{4}$）×|-24|
（3）8-23÷（-4）3-$\frac{1}{8}$
（4）（-5）×6+（-125）÷（-5）
（5）-64÷3$\frac{1}{5}$×（-$\frac{5}{8}$）
（6）1-$\frac{1}{2}$×[3×（-$\frac{2}{3}$）2-（-1）3]+$\frac{1}{4}$÷（-$\frac{1}{2}$）2．
8．-2的绝对值是2；-2的倒数是-$\frac{1}{2}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网