题目内容
6.在△ABC中,∠A,∠B,∠C的对应边分别为a,b,c,若∠A+∠C=90°,则( )| A. | a2+b2=c2 | B. | a2+c2=b2 | C. | b2+c2=a2 | D. | a=c |
分析 结合三角形内角和定理得到∠B=90°,所以由勾股定理可以直接得到答案.
解答 解:∵在△ABC中,∠A+∠C=90°,
∴∠B=90°,
∴a2+c2=b2.
故选:B.
点评 本题考查了勾股定理.注意:勾股定理应用的前提条件是在直角三角形中.

练习册系列答案
相关题目
14.下列计算正确的是( )
| A. | (±$\frac{1}{4}$)2=$\frac{1}{2}$ | B. | ±($\sqrt{1\frac{9}{16}}$)=±1$\frac{1}{4}$ | C. | -$\sqrt{0.9}$=-0.3 | D. | $\sqrt{1{3}^{2}-{7}^{2}}$=6 |
1.在4-10-8中,把省略的“+”填上,正确的是( )
| A. | 4+10+8 | B. | -4+(-10)+(-8) | C. | 4-(+10)-(+8) | D. | 4+(-10)+(-8) |
11.长方形的周长为a cm,长为b cm,则长方形的宽为( )
| A. | (a-2b) cm | B. | ($\frac{a}{2}$-2b) cm | C. | $\frac{a-b}{2}$ cm | D. | $\frac{a-2b}{2}$ cm |
18.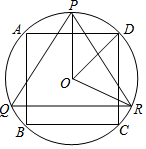 如图,△PQR是⊙O的内接正三角形,四边形ABCD是⊙O的内接正方形,BC∥QR,则∠DOR的度数是( )
如图,△PQR是⊙O的内接正三角形,四边形ABCD是⊙O的内接正方形,BC∥QR,则∠DOR的度数是( )
 如图,△PQR是⊙O的内接正三角形,四边形ABCD是⊙O的内接正方形,BC∥QR,则∠DOR的度数是( )
如图,△PQR是⊙O的内接正三角形,四边形ABCD是⊙O的内接正方形,BC∥QR,则∠DOR的度数是( )| A. | 60 | B. | 65 | C. | 72 | D. | 75 |
15.下列说法错误的是( )
| A. | 平行四边形的对角相等 | |
| B. | 正方形的对称轴有四条 | |
| C. | 矩形既是中心对称图形又是轴对称图形 | |
| D. | 菱形的对角线相等且互相平分 |
16.若a<0,b<0,则下列各式正确的是( )
| A. | a-b<0 | B. | a-b>0 | C. | a-b=0 | D. | ab>0 |
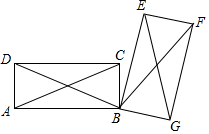 如图,把矩形ABCD绕点B顺时针旋转得到矩形EBGF,则图中与线段AC相等的线段有( )条.
如图,把矩形ABCD绕点B顺时针旋转得到矩形EBGF,则图中与线段AC相等的线段有( )条.