题目内容
7.(1)(-5)+2$\frac{2}{3}$+(-$\frac{1}{2}$)+(-2$\frac{2}{3}$)(2)(-$\frac{1}{2}$+$\frac{2}{3}$-$\frac{1}{4}$)×|-24|
(3)8-23÷(-4)3-$\frac{1}{8}$
(4)(-5)×6+(-125)÷(-5)
(5)-64÷3$\frac{1}{5}$×(-$\frac{5}{8}$)
(6)1-$\frac{1}{2}$×[3×(-$\frac{2}{3}$)2-(-1)3]+$\frac{1}{4}$÷(-$\frac{1}{2}$)2.
分析 (1)先算同分母分数,再算加减法;
(2)根据乘法分配律计算;
(3)(6)先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.
(4)先算乘除,后算加法;
(5)将除法变为乘法,再约分计算即可求解.
解答 解:(1)(-5)+2$\frac{2}{3}$+(-$\frac{1}{2}$)+(-2$\frac{2}{3}$)
=-5+(2$\frac{2}{3}$-2$\frac{2}{3}$)+(-$\frac{1}{2}$)
=-5+0-$\frac{1}{2}$
=-5$\frac{1}{2}$;
(2)(-$\frac{1}{2}$+$\frac{2}{3}$-$\frac{1}{4}$)×|-24|
=(-$\frac{1}{2}$+$\frac{2}{3}$-$\frac{1}{4}$)×24
=-$\frac{1}{2}$×24+$\frac{2}{3}$×24-$\frac{1}{4}$×24
=-12+16-6
=-2;
(3)8-23÷(-4)3-$\frac{1}{8}$
=8-8÷(-64)-$\frac{1}{8}$
=8+$\frac{1}{8}$-$\frac{1}{8}$
=8;
(4)(-5)×6+(-125)÷(-5)
=-30+25
=-5;
(5)-64÷3$\frac{1}{5}$×(-$\frac{5}{8}$)
=-64×$\frac{5}{16}$×(-$\frac{5}{8}$)
=12$\frac{1}{2}$;
(6)1-$\frac{1}{2}$×[3×(-$\frac{2}{3}$)2-(-1)3]+$\frac{1}{4}$÷(-$\frac{1}{2}$)2.
=1-$\frac{1}{2}$×[3×$\frac{4}{9}$-(-1)]+$\frac{1}{4}$÷$\frac{1}{4}$
=1-$\frac{1}{2}$×[$\frac{4}{3}$-(-1)]+1
=1-$\frac{1}{2}$×$\frac{7}{3}$+1
=1-$\frac{7}{6}$+1
=$\frac{5}{6}$.
点评 考查了有理数的混合运算,有理数混合运算的四种运算技巧:1.转化法:一是将除法转化为乘法,二是将乘方转化为乘法,三是在乘除混合运算中,通常将小数转化为分数进行约分计算. 2.凑整法:在加减混合运算中,通常将和为零的两个数,分母相同的两个数,和为整数的两个数,乘积为整数的两个数分别结合为一组求解. 3.分拆法:先将带分数分拆成一个整数与一个真分数的和的形式,然后进行计算. 4.巧用运算律:在计算中巧妙运用加法运算律或乘法运算律往往使计算更简便.

 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案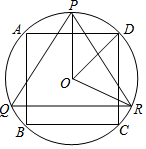 如图,△PQR是⊙O的内接正三角形,四边形ABCD是⊙O的内接正方形,BC∥QR,则∠DOR的度数是( )
如图,△PQR是⊙O的内接正三角形,四边形ABCD是⊙O的内接正方形,BC∥QR,则∠DOR的度数是( )| A. | 60 | B. | 65 | C. | 72 | D. | 75 |
| A. | 平行四边形的对角相等 | |
| B. | 正方形的对称轴有四条 | |
| C. | 矩形既是中心对称图形又是轴对称图形 | |
| D. | 菱形的对角线相等且互相平分 |
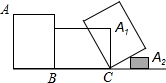 如图,长方形木板的长为4cm,宽为3cm,某同学使之在桌面上做无滑动的翻滚(顺时针方向),木板上点A的位置变化为A→Al→A2,其中第二次翻滚被桌面上的一块小木板挡住,使木板与桌面成30°,则点A滚到A2位置时走过的路径总长为( )
如图,长方形木板的长为4cm,宽为3cm,某同学使之在桌面上做无滑动的翻滚(顺时针方向),木板上点A的位置变化为A→Al→A2,其中第二次翻滚被桌面上的一块小木板挡住,使木板与桌面成30°,则点A滚到A2位置时走过的路径总长为( )| A. | 10cm | B. | 3.5π cm | C. | 4.5π cm | D. | 2.5π cm |
| A. | a-b<0 | B. | a-b>0 | C. | a-b=0 | D. | ab>0 |
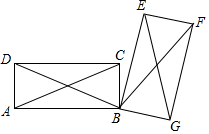 如图,把矩形ABCD绕点B顺时针旋转得到矩形EBGF,则图中与线段AC相等的线段有( )条.
如图,把矩形ABCD绕点B顺时针旋转得到矩形EBGF,则图中与线段AC相等的线段有( )条.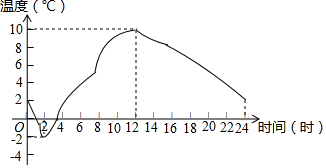 如图是某地区春季某天的气温随时间的变化图象.请根据图象回答:
如图是某地区春季某天的气温随时间的变化图象.请根据图象回答: