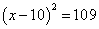题目内容
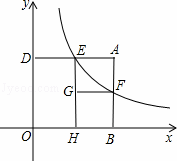
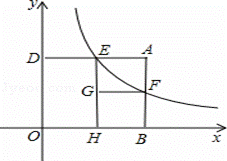
如图,矩形ABOD的两边OB,OD都在坐标轴的正半轴上,OD=3,另两边与反比例函数的图 象分别相交于点E,F,且DE=2.过点E作EH⊥x轴于点H,过点F作FG⊥EH于点G.回答下面的问题:
象分别相交于点E,F,且DE=2.过点E作EH⊥x轴于点H,过点F作FG⊥EH于点G.回答下面的问题:
(1)该反比例函数的解析式是什么?
(2)当四边形AEGF为正方形时,点F的坐标时多少?
(3)阅读合作学习内容,请解答其中的问题;
小亮进一步研究四边形A EGF的特征后提出问题:“当AE>EG时,矩形AEGF与矩形DOHE能否全等?能否相似?”
EGF的特征后提出问题:“当AE>EG时,矩形AEGF与矩形DOHE能否全等?能否相似?”
针对小亮提出的问题,请你判断这两个矩形能否全等?直接写出结论即可;这两个矩形能否相似?若能相似,求出相似比;若不能相似,试说明理由.

解答:
解:(1)∵四边形ABOD为矩形,EH⊥x轴,
而OD=3,DE=2,
∴E点坐标为(2,3),
∴k=2×3=6,
∴反比例函数解析式为y=6/x(x>0);--------------2分
(2)设正方形AEGF的边长为a,则AE=AF=6,
∴B点坐标为(2+a,0)),A点坐标为(2+a,3),
∴F点坐标为(2+a,3﹣a),--------------4分
把F(2+a,3﹣a)代入y=得(2+a)(3﹣a)=6,解得a1=1,a2=0(舍去),
∴F点坐标为(3,2);--------------6分
(3)当AE>EG时,矩形AEGF与矩形DOHE不能全等.--------------7分
当AE> EG时,矩形AEGF与矩形DOHE能相似.--------------8分
EG时,矩形AEGF与矩形DOHE能相似.--------------8分
∵矩形AEGF与矩形DOHE能相似,
∴AE:OD=AF:DE,
∴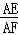 =
=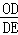 =3\2,
=3\2,
设AE=3t,则AF=2t,
∴A点坐标为(2+3t,3),
∴F点坐标为(2+3t,3﹣2t),--------------10分
把F(2+3t,3﹣2t)代入y=得(2+3t)(3﹣2t)=6,解得t1=0(舍去),t2=5\6,
∴AE=3t=5\2,
∴相似比=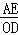 =5\6--------------12分
=5\6--------------12分
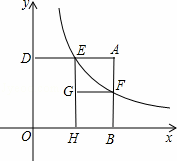

 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 (
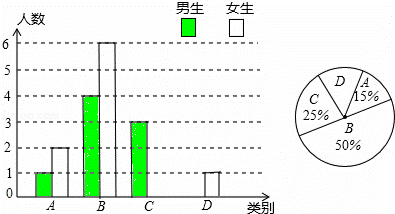
( )的大致图象如图所示,关于该二次函数,下列说法不正确的是( )
)的大致图象如图所示,关于该二次函数,下列说法不正确的是( ) 随
随 的增大而减少
的增大而减少 D、当
D、当 时,
时,

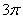 B.
B. C.
C. D.
D.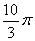
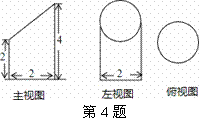
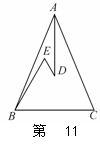
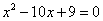 ,配方后可得
,配方后可得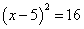 B.
B. 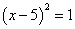 C.
C. 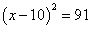 D.
D.