题目内容
5.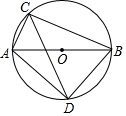 如图,AB是⊙O的直径,弦BC长为$4\sqrt{2}$,弦AC长为2,∠ACB的平分线交⊙O于点D.
如图,AB是⊙O的直径,弦BC长为$4\sqrt{2}$,弦AC长为2,∠ACB的平分线交⊙O于点D.(1)求AD的长.
(2)求CD的长.
分析 (1)由AB是⊙O的直径,可得∠ACB=∠ADB=90°,然后由勾股定理求得AB的长,又由∠ACB的平分线交⊙O于点D,易得△ABD是等腰直角三角形,则可求得答案;
(2)过点D分别作DM⊥CA于M,DN⊥CB于N,可证DM=DN,再证Rt△DAM≌Rt△DBN,得AM=BN,易证正方形DMCB,故CM=CN,然后设AM=x,可得方程$4\sqrt{2}-x=2+x$,继而求得答案.
解答 解:(1)∵AB是直径,
∴∠ACB=∠ADB=90°,
在Rt△ABC中,
∴$AB=\sqrt{A{C^2}+B{C^2}}=\sqrt{{2^2}+{{(4\sqrt{2})}^2}}=6$,
∵∠ACB的平分线交⊙O于点D,
∴∠DCA=∠BCD,
∴$\widehat{AD}$=$\widehat{BD}$,
∴AD=BD=$\frac{{\sqrt{2}}}{2}AB=3\sqrt{2}$,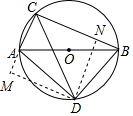 (2)过点D分别作DM⊥CA于M,DN⊥CB于N,
(2)过点D分别作DM⊥CA于M,DN⊥CB于N,
∵∠ACB的平分线交⊙O于点D,
∴DM=DN,
在Rt△DAM和Rt△DBN中,
$\left\{\begin{array}{l}{DM=DN}\\{AD=BD}\end{array}\right.$,
∴Rt△DAM≌Rt△DBN(HL)),
∴AM=BN,
∴四边形BDMC是正方形DMCB,
∴CM=CN,
设AM=x,
则$4\sqrt{2}-x=2+x$,
解得:$x=2\sqrt{2}-1$,
∴$CD=\sqrt{2}MC=4+\sqrt{2}$.
点评 此题考查了圆周角定理、勾股定理、全等三角形的判定与性质以及正方形的判定与性质.注意准确作出辅助线是解此题的关键.

练习册系列答案
 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目
10.下列各对数中,互为相反数的是( )
| A. | +(-2)和-2 | B. | -(-2)和-|-2| | C. | -(-2)和|-2| | D. | -(-2)和+(+2) |
 请你帮小明把下面的证明过程补充完整.
请你帮小明把下面的证明过程补充完整.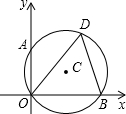 如图,⊙C经过原点且与两坐标轴分别交于点A和点B,点A的坐标为(0,2),D为⊙C在第一象限内的一点且∠ODB=60°,解答下列各题:
如图,⊙C经过原点且与两坐标轴分别交于点A和点B,点A的坐标为(0,2),D为⊙C在第一象限内的一点且∠ODB=60°,解答下列各题: 如图所示,根据几何体的三视图及其尺寸解答下列问题
如图所示,根据几何体的三视图及其尺寸解答下列问题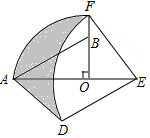 如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是8-π.
如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是8-π.