题目内容
在平面直角坐标系中,有A(3,3),B(1,-1)两点,现在y轴上取一点P,当P点的坐标为 时,AP+BP的值最小.
考点:轴对称-最短路线问题,坐标与图形性质
专题:
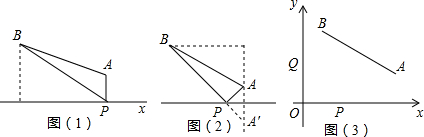
分析:作B点关于y轴对称点B′点,连接AB′,交y轴于点P,则此时AP+PB最小,进而利用勾股定理求出PA+PB的最小值.
解答: 解:如图所示:作B点关于y轴对称点B′点,
解:如图所示:作B点关于y轴对称点B′点,
连接AB′,交y轴于点P,则此时AP+PB最小,
∵B(1,-1),
∴B′(-1,-1),
设直线AB′的解析式为y=kx+b,
∵A(3,3),
∴
,解得
,
∴直线AB′的解析式为y=x,
∴直线y=x与y轴的交点P为(0,0).
故答案为(0,0).
 解:如图所示:作B点关于y轴对称点B′点,
解:如图所示:作B点关于y轴对称点B′点,连接AB′,交y轴于点P,则此时AP+PB最小,
∵B(1,-1),
∴B′(-1,-1),
设直线AB′的解析式为y=kx+b,
∵A(3,3),
∴
|
|
∴直线AB′的解析式为y=x,
∴直线y=x与y轴的交点P为(0,0).
故答案为(0,0).
点评:此题主要考查了利用轴对称求最短路线以及坐标和图形的关系,得出P点位置是解题关键.

练习册系列答案
相关题目
 已知△ABC中,AB=AC,∠ABC=60°,P是AC上一点,D是BC延长线上一点,且PB=PD,过D点作DE⊥AC,交AC延长线于点E,求AP与CE之间的数量关系.
已知△ABC中,AB=AC,∠ABC=60°,P是AC上一点,D是BC延长线上一点,且PB=PD,过D点作DE⊥AC,交AC延长线于点E,求AP与CE之间的数量关系. 如图,已知点A的坐标为(-16,0),过点A的直线交y轴于点C,OB⊥AC于点B,
如图,已知点A的坐标为(-16,0),过点A的直线交y轴于点C,OB⊥AC于点B,