题目内容
如图,AB=50km,AB到沪渝高速公路直线X的距离分别为10km和40km,要在沪渝高速公路旁修建一服务区P,向A、B两景区运送游客.小民设计了两种方案,图(1)是方案一的示意图(AP与直线X垂直,垂足为P),P到A、的距离之和S1=PA+PB,图(2)是方案二的示意图(点A关于直线X的对称点是A′,连接B′A′交直线X于点P),P到A、B的距离之和S2=PA+PB.
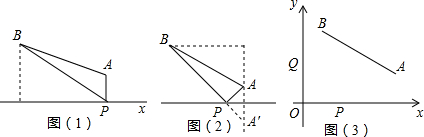
(1)求S1、S2,并比较它们的大小;
(2)请你说明S2=PA+PB的值为最小;
(3)假设另外一条高速公路Y与沪渝高速公路垂直,如图(3),B 到直线Y的距离为30km,请你在X旁和Y旁各修建一服务区P、Q,使P、A、B、Q组成的四边形的周长最小.并求出这个最小值.

(1)求S1、S2,并比较它们的大小;
(2)请你说明S2=PA+PB的值为最小;
(3)假设另外一条高速公路Y与沪渝高速公路垂直,如图(3),B 到直线Y的距离为30km,请你在X旁和Y旁各修建一服务区P、Q,使P、A、B、Q组成的四边形的周长最小.并求出这个最小值.
考点:轴对称-最短路线问题,作图—应用与设计作图
专题:
分析:(1)根据勾股定理分别求得S1、S2的值,比较即可;
(2)在公路上任找一点M,连接MA,MB,MA',由轴对称知MA=MA,∴MB+MA=MB+MA'>A'B,∴S2=BA'为最小;
(3)过A作关于X轴的对称点A',过B作关于Y轴的对称点B',连接A'B',交X轴于点P,交Y轴于点Q,求出A'B'的值即可.在公路上任找一点M,连接MA,MB,MA',由轴对称知MA=MA,∴MB+MA=MB+MA'>A'B,∴S2=BA'为最小;
(2)在公路上任找一点M,连接MA,MB,MA',由轴对称知MA=MA,∴MB+MA=MB+MA'>A'B,∴S2=BA'为最小;
(3)过A作关于X轴的对称点A',过B作关于Y轴的对称点B',连接A'B',交X轴于点P,交Y轴于点Q,求出A'B'的值即可.在公路上任找一点M,连接MA,MB,MA',由轴对称知MA=MA,∴MB+MA=MB+MA'>A'B,∴S2=BA'为最小;
解答: 解:(1)图(1)中过B作BC⊥X于C,垂足为C;AD⊥BC于D,垂足为D,
解:(1)图(1)中过B作BC⊥X于C,垂足为C;AD⊥BC于D,垂足为D,
则BC=40km,
又∵AP=10,
∴BD=BC-CD=40-10=30km.
在△ABD中,AD=
=40km,
在Rt△PBC中,
∴BP=
=40
km,
S1=40
+10(km).
图(2)中,过B作BC⊥AA′垂足为C,则A′C=50km,
又∵BC=40km,
∴BA'=
=10
km,
由轴对称知:PA=PA',
∴S2=BA'=10
km,
∴S1>S2.
(2)如图(2),在公路上任找一点M,连接MA,MB,MA',由轴对称知MA=MA',
∴MB+MA=MB+MA'>A'B,
∴S2=BA'为最小.

(3)过A作关于X轴的对称点A',过B作关于Y轴的对称点B',
连接A'B',交X轴于点P,交Y轴于点Q,则P,Q即为所求.
过A'、B'分别作X轴、Y轴的平行线交于点G,
B′G=40+10=50km,A′G=30+30+40=100km,
A'B'=
=50
km,
∴AB+AP+BQ+QP=AB+A′P+PQ+B′Q=50+50
km,
∴所求四边形的周长为(50+50
)km.
 解:(1)图(1)中过B作BC⊥X于C,垂足为C;AD⊥BC于D,垂足为D,
解:(1)图(1)中过B作BC⊥X于C,垂足为C;AD⊥BC于D,垂足为D,则BC=40km,
又∵AP=10,
∴BD=BC-CD=40-10=30km.
在△ABD中,AD=
| 502-302 |
在Rt△PBC中,
∴BP=
| CP2+BC2 |
| 2 |
S1=40
| 2 |
图(2)中,过B作BC⊥AA′垂足为C,则A′C=50km,
又∵BC=40km,
∴BA'=
| 402+502 |
| 41 |
由轴对称知:PA=PA',
∴S2=BA'=10
| 41 |

∴S1>S2.
(2)如图(2),在公路上任找一点M,连接MA,MB,MA',由轴对称知MA=MA',
∴MB+MA=MB+MA'>A'B,
∴S2=BA'为最小.

(3)过A作关于X轴的对称点A',过B作关于Y轴的对称点B',
连接A'B',交X轴于点P,交Y轴于点Q,则P,Q即为所求.
过A'、B'分别作X轴、Y轴的平行线交于点G,
B′G=40+10=50km,A′G=30+30+40=100km,
A'B'=
| 1002+502 |
| 5 |
∴AB+AP+BQ+QP=AB+A′P+PQ+B′Q=50+50
| 5 |
∴所求四边形的周长为(50+50
| 5 |
点评:此题考查了线路最短的问题,确定动点为何位置是关键,综合运用勾股定理的知识.

练习册系列答案
相关题目
 在锐角△ABC中,∠ABC=45°,CD⊥AB,D是垂足,BD=4,M、N分别是BD、BC上动点,则CM+MN的最小值是
在锐角△ABC中,∠ABC=45°,CD⊥AB,D是垂足,BD=4,M、N分别是BD、BC上动点,则CM+MN的最小值是