题目内容
下面网格图中,每个小正方形的边长均为1,每个小格的顶点叫格点.
(1)请在图1中,画一个格点三角形,使它的三边长都是有理数;
(2)请在图2中,画一个格点三角形,使它的三边长都是无理数;
(3)图3中的△ABC的面积为 ,AB边上的高为 .
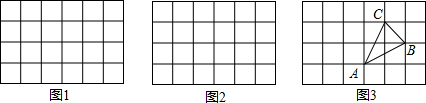
(1)请在图1中,画一个格点三角形,使它的三边长都是有理数;
(2)请在图2中,画一个格点三角形,使它的三边长都是无理数;
(3)图3中的△ABC的面积为

考点:勾股定理
专题:作图题
分析:(1)利用勾股数是3,4,5的三边可以租成三角形即可得到格点三角形;
(2)利用勾股定理,找长为无理数的线段,画三角形即可;
(3)利用△ABC所在的矩形的面积减去四周三个直角三角形的面积,列式进行计算即可得解,再由△ABC的面积为定值即可求出AB边上的高.
(2)利用勾股定理,找长为无理数的线段,画三角形即可;
(3)利用△ABC所在的矩形的面积减去四周三个直角三角形的面积,列式进行计算即可得解,再由△ABC的面积为定值即可求出AB边上的高.
解答:解:(1)(2)如图所示:

(3)△ABC的面积=2×2-
×1×2-
×2×1-
×1×1=4-1-1-
=1.5,
因为AB•h=BC•h′,
所以h=
=
,
故答案为:1.5,
.

(3)△ABC的面积=2×2-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
因为AB•h=BC•h′,
所以h=
| BC•h′ |
| AB |
2
| ||
| 3 |
故答案为:1.5,
2
| ||
| 3 |
点评:本题考查了勾股定理的运用,熟练掌握网格结构的特点以及勾股定理是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 如图所示,AD是∠BAC的平分线,P为BC延长线上一点,且PA=PD.求证:PA与⊙O相切.
如图所示,AD是∠BAC的平分线,P为BC延长线上一点,且PA=PD.求证:PA与⊙O相切.