题目内容

“对角线不相等的四边形不是矩形”，这个命题用反证法证明应假设
 
．
考点：反证法
专题：
分析：利用反证法的一般步骤是：
①假设命题的结论不成立；
②从这个假设出发，经过推理论证，得出矛盾；
③由矛盾判定假设不正确，从而肯定原命题的结论正确，进而得出答案即可．
解答：解：“对角线不相等的四边形不是矩形”，这个命题用反证法证明应假设该四边形是矩形．
故答案为：该四边形是矩形．
点评：此题主要考查了反证法，正确掌握反证法的步骤是解题关键．
练习册系列答案
相关题目
阅读理解：
如图1，点C将线段AB分成两部分，若
AC
AB
=
BC
AC
，则点C为线段AB的黄金分割点．
某研究学习小组，由黄金分割点联想到“黄金分割线”，而给出“黄金分割线”的定义：直线l将一个面积为S的图形分成两部分，这两部分的面积分别为S1、S2，如果
S1
S
=
S2
S1
，那么称直线l为该图形的黄金分割线．
问题解决：
如图2，在△ABC中，若点D是AB的黄金分割点．
（1）研究小组猜想：直线CD是△ABC的黄金分割线，你认为对吗？为什么？
（2）请你说明：三角形的中线是否也是该三角形的黄金分割线？
（3）研究小组探究发现：过点C作直线交AB于E，过D作DF∥CE，交AC于F，连接EF（如图3），则直线EF也是△ABC的黄金分割线．请你说明理由． 
已知a=
1
2013
+2012，b=
1
2013
+2013，c=
1
2013
+2014，则代数式2（a2+b2+c2-ab-bc-ac）的值是
 
．
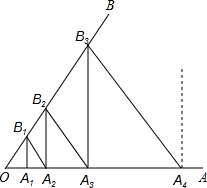如图，已知∠AOB=60°，在OA上取OA1=1，过点A1作A1B1⊥OA交OB于点B1，过点B1作B1A2⊥OB交OA于点A2，过点A2作A2B2⊥OA交OB于点B2，过点B2作B2A3⊥OB交OA于点A3，…，按此作法继续下去，则OA10的值是
 
．
在?ABCD中，AC=6、BD=4，则AB的取值范围是
 
．
△ABC的周长是24cm，面积是32cm2，则它的三条中位线所围成的三角形的周长是
 
cm，面积是
 
cm2．
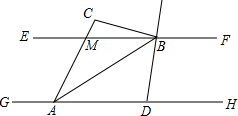如图，已知EF∥GH，A、D为GH上的两点，M、B为EF上的两点，延长AM于点C，AB平分∠DAC，直线DB平分∠FBC，若∠ACB=100°，则∠DBA的度数为
 
．
若3，a，4，5的中位数是4，则这组数据的方差是
 
．
已知P（a，b）在反比函数的y=
2
x
的图象上，若P关于y轴对称的点在反比例函数y=
k
x
的图象上，则k的值是（　　）
A、-2B、-1C、1D、2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网