Question

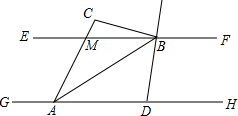如图，已知EF∥GH，A、D为GH上的两点，M、B为EF上的两点，延长AM于点C，AB平分∠DAC，直线DB平分∠FBC，若∠ACB=100°，则∠DBA的度数为

 

．

Answer 1

考点：平行线的性质

专题：

分析：根据两直线平行，内错角相等可得∠2=∠3，再根据三角形的内角和定理表示出∠4，然后表示∠5，再利用平角等于180°列式表示出∠DBA整理即可得解．

解答：解：
如图，设∠DAB=∠BAC=x，即∠1=∠2=x，
∵EF∥GH，
∴∠2=∠3，
在△ABC内，∠4=180°-∠ACB-∠1-∠3=180°-∠ACB-2x，
∵直线BD平分∠FBC，
∴∠5=

1

2

（180°-∠4）=

1

2

（180°-180°+∠ACB+2x）=

1

2

∠ACB+x，
∴∠DBA=180°-∠3-∠4-∠5
=180°-x-（180°-∠ACB-2x）-（

1

2

∠ACB+x）
=180°-x-180°+∠ACB+2x-

1

2

∠ACB-x
=

1

2

∠ACB
=

1

2

×100°
=50°．
故答案为：50°．

点评：本题考查了平行线的性质，角平分线的定义，三角形的内角和定理，熟记性质并理清图中各角度之间的关系是解题的关键．