题目内容
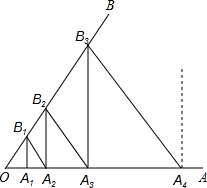 如图,已知∠AOB=60°,在OA上取OA1=1,过点A1作A1B1⊥OA交OB于点B1,过点B1作B1A2⊥OB交OA于点A2,过点A2作A2B2⊥OA交OB于点B2,过点B2作B2A3⊥OB交OA于点A3,…,按此作法继续下去,则OA10的值是
如图,已知∠AOB=60°,在OA上取OA1=1,过点A1作A1B1⊥OA交OB于点B1,过点B1作B1A2⊥OB交OA于点A2,过点A2作A2B2⊥OA交OB于点B2,过点B2作B2A3⊥OB交OA于点A3,…,按此作法继续下去,则OA10的值是考点:含30度角的直角三角形
专题:规律型
分析:根据直角三角形两锐角互余求出∠OB1A1=∠OA2B1=30°,再根据直角三角形30°角所对的直角边等于斜边的一半求出OB1、OA2,然后同理求解即可.
解答:解:∵∠AOB=60°,A1B1⊥OA,B1A2⊥OB,
∴∠OB1A1=∠OA2B1=90°-∠AOB=90°-60°=30°,
∴OB1=2OA1=2×1=2,
OA2=2OB1=2×2=4,
同理可得,OB2=2OA2=2×4=8,
OA3=2OB2=2×8=16=42,
…,
OA10=49.
故答案为:49.
∴∠OB1A1=∠OA2B1=90°-∠AOB=90°-60°=30°,
∴OB1=2OA1=2×1=2,
OA2=2OB1=2×2=4,
同理可得,OB2=2OA2=2×4=8,
OA3=2OB2=2×8=16=42,
…,
OA10=49.
故答案为:49.
点评:本题考查了直角三角形30°角所对的直角边等于斜边的一半的性质,直角三角形两锐角互余的性质,熟记性质是解题的关键.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
下列各式是最简二次根式的是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,已知点A1,A2,…,A2011在函数y=x2位于第二象限的图象上,点B1,B2,…,B2011在函数y=x2位于第一象限的图象上,点C1,C2,…,C2011在y轴的正半轴上,若四边形OA1C1B1、C1A2C2B2,…,C2010A2011C2011B2011都是正方形,则正方形C2010A2011C2011B2011的边长为
如图,已知点A1,A2,…,A2011在函数y=x2位于第二象限的图象上,点B1,B2,…,B2011在函数y=x2位于第一象限的图象上,点C1,C2,…,C2011在y轴的正半轴上,若四边形OA1C1B1、C1A2C2B2,…,C2010A2011C2011B2011都是正方形,则正方形C2010A2011C2011B2011的边长为 如图,已知A点是反比例函数y=
如图,已知A点是反比例函数y=