题目内容
研究发现,二次函数y=ax2(a≠0)图象上任何一点到定点(0,
)和到定直线y=-
的距离相等.我们把定点(0,
)叫做抛物线y=ax2的焦点,定直线y=-
叫做抛物线y=ax2的准线.
(1)写出函数y=
x2图象的焦点坐标和准线方程;
(2)等边三角形OAB的三个顶点都在二次函数y=
x2图象上,O为坐标原点,求等边三角形的边长;
(3)M为抛物线y=
x2上的一个动点,F为抛物线y=
x2的焦点,P(1,3)为定点,求MP+MF的最小值.
| 1 |
| 4a |
| 1 |
| 4a |
| 1 |
| 4a |
| 1 |
| 4a |
(1)写出函数y=
| 1 |
| 4 |
(2)等边三角形OAB的三个顶点都在二次函数y=
| 1 |
| 4 |
(3)M为抛物线y=
| 1 |
| 4 |
| 1 |
| 4 |
考点:二次函数综合题
专题:综合题
分析:(1)根据焦点坐标为(0,
),准线方程为y=-
,即可得出答案.
(2)根据题意可设A(x,y),B(-x,y),从而根据等边三角形及抛物线的性质可得出∠AOE=30°,继而可得出|y|=
|x|,代入可得出x和y的值,也可求出等边三角形的边长.
(3)点P到点F的距离等于点P到准线的距离,从而根据垂线段最短的知识可找到点M的位置,结合图形可得出这个最小值.
| 1 |
| 4a |
| 1 |
| 4a |
(2)根据题意可设A(x,y),B(-x,y),从而根据等边三角形及抛物线的性质可得出∠AOE=30°,继而可得出|y|=
| 3 |
(3)点P到点F的距离等于点P到准线的距离,从而根据垂线段最短的知识可找到点M的位置,结合图形可得出这个最小值.
解答:解:(1)由题意得,焦点坐标为:(0,1),准线方程为:y=-1;
(2)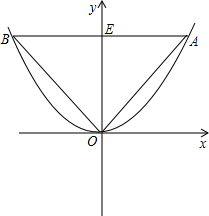
设A(x,y),B(-x,y),
∵△OAB是等边三角形,
∴∠AOE=
∠AOB=30°,
∴y=
x,
将点A坐标(x,y)=(x,
x)代入函数解析式,可得
x=
x2,
解得:x=4
,
故可得点A坐标为(4
,12),三角形的边长=OA=
=8
.
(3)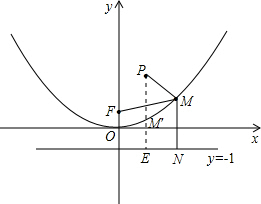
过点M作MN⊥准线,交准线于点N,
则由题意可得,MN=MF,
故可得:MP+MF=MP+MN,
结合图形可得过点P作PE⊥准线,交准线于点E,则PE于抛物线的交点M'能满足MP+MF最小,
此时M'P+M'F=PE=4.
(2)

设A(x,y),B(-x,y),
∵△OAB是等边三角形,
∴∠AOE=
| 1 |
| 2 |
∴y=
| 3 |
将点A坐标(x,y)=(x,
| 3 |
| 3 |
| 1 |
| 4 |
解得:x=4
| 3 |
故可得点A坐标为(4
| 3 |
122+(4
|
| 3 |
(3)

过点M作MN⊥准线,交准线于点N,
则由题意可得,MN=MF,
故可得:MP+MF=MP+MN,
结合图形可得过点P作PE⊥准线,交准线于点E,则PE于抛物线的交点M'能满足MP+MF最小,
此时M'P+M'F=PE=4.
点评:此题考查了二次函数的综合题,解答本题的关键是仔细审题得出函数的准线与焦点,综合性较强,注意解答过程中将所学知识融会贯通.

练习册系列答案
相关题目
在平行四边形、矩形、菱形、等腰梯形中任选两个图形,那么下列事件中为不可能事件的是( )
| A、这两个图形都是中心对称图形 |
| B、这两个图形都不是中心对称图形 |
| C、这两个图形都是轴对称图形 |
| D、这两个图形都是轴对称图形又是中心对称图形 |
当n取遍大于1的所有自然数时,下列四个式子中所取的代数值总不出现完全平方数的是( )
| A、5n2-5n-5 |
| B、3n2-3n+3 |
| C、9n2-9n+9 |
| D、11n2-11n-11 |