题目内容
10.已知等腰三角形的周长为60cm,腰长为xcm,底边长为ycm,那么y与x的函数解析式为y=-2x+60,定义域为15<x<30.分析 根据底边长+两腰长=周长,建立等量关系,变形即可,再根据三角形两边之和大于第三边及周长的限制,确定自变量的取值范围.
解答 解:依题意得2x+y=60,
即y=-2x+60;
根据三角形的三边关系得:$\left\{\begin{array}{l}{x+x>-2x+60}\\{-2x+60>0}\end{array}\right.$,
解得:15<x<30.
故答案为:y=-2x+60,15<x<30.
点评 本题考查了函数关系式、等腰三角形三边关系的性质、三角形三边关系定理,得出y与x的函数关系式是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.小明沿着坡角为40°的坡面向下走了m米,那么他下降( )米.
| A. | msin40° | B. | mcos40° | C. | mtan40° | D. | $\frac{m}{tan40°}$ |
18.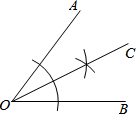 如图,用直尺和圆规作一个角的平分线,是运用了“全等三角形的对应角相等”这一性质,由作图所得条件,判定三角形全等运用的方法是( )
如图,用直尺和圆规作一个角的平分线,是运用了“全等三角形的对应角相等”这一性质,由作图所得条件,判定三角形全等运用的方法是( )
 如图,用直尺和圆规作一个角的平分线,是运用了“全等三角形的对应角相等”这一性质,由作图所得条件,判定三角形全等运用的方法是( )
如图,用直尺和圆规作一个角的平分线,是运用了“全等三角形的对应角相等”这一性质,由作图所得条件,判定三角形全等运用的方法是( )| A. | SSS | B. | ASA | C. | AAS | D. | SAS |
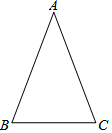 定理:等腰三角形的两个底角相等(简称“等边对等角”).
定理:等腰三角形的两个底角相等(简称“等边对等角”).