题目内容
1.解关于x的不等式:($\frac{1}{2}$-a)x>1-2a.分析 先对原不等式变形,然后讨论1-2a的正负情况即可解答本题.
解答 解:($\frac{1}{2}$-a)x>1-2a
$\frac{1-2a}{2}•x>1-2a$
(1-2a)x>2(1-2a)
当1-2a>0时,即a<$\frac{1}{2}$时,x>2;
当1-2a=0时,即a=$\frac{1}{2}$时,x无解;
当1-2a<0时,即a>$\frac{1}{2}$时,x<2;
则a<$\frac{1}{2}$时,原不等式的解集是x>2;
a=$\frac{1}{2}$时,原不等式无解;
a>$\frac{1}{2}$时,原不等式的解集是x<2.
点评 本题考查解一元一次不等式,解题的关键是明确解一元一次不等式的方法,利用分类讨论的数学思想解答.

练习册系列答案
相关题目
11.若a>0,且ax=3,ay=2,则a2x-y的值为( )
| A. | 3 | B. | 4 | C. | $\frac{9}{2}$ | D. | 7 |
13. 如图所示,该几何体的俯视图是( )
如图所示,该几何体的俯视图是( )
 如图所示,该几何体的俯视图是( )
如图所示,该几何体的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
10.小明用计算器计算(a+b)c的值,其按键顺序和计算器显示结果如表:

这时他才明白计算器是先做乘法再做加法的,于是他依次按键:

从而得到了正确结果,已知a是b的3倍,则正确的结果是( )

这时他才明白计算器是先做乘法再做加法的,于是他依次按键:

从而得到了正确结果,已知a是b的3倍,则正确的结果是( )
| A. | 24 | B. | 39 | C. | 48 | D. | 96 |
11.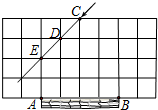 足球射门,不考虑其他因素,仅考虑射点到球门AB的张角大小时,张角越大,射门越好.如图的正方形网格中,点A,B,C,D,E均在格点上,球员带球沿CD方向进攻,最好的射点在( )
足球射门,不考虑其他因素,仅考虑射点到球门AB的张角大小时,张角越大,射门越好.如图的正方形网格中,点A,B,C,D,E均在格点上,球员带球沿CD方向进攻,最好的射点在( )
 足球射门,不考虑其他因素,仅考虑射点到球门AB的张角大小时,张角越大,射门越好.如图的正方形网格中,点A,B,C,D,E均在格点上,球员带球沿CD方向进攻,最好的射点在( )
足球射门,不考虑其他因素,仅考虑射点到球门AB的张角大小时,张角越大,射门越好.如图的正方形网格中,点A,B,C,D,E均在格点上,球员带球沿CD方向进攻,最好的射点在( )| A. | 点C | B. | 点D或点E | ||
| C. | 线段DE(异于端点) 上一点 | D. | 线段CD(异于端点) 上一点 |




 如图,已知∠1=∠2,∠A=∠3,能否判断AB∥CD?说明你的理由.
如图,已知∠1=∠2,∠A=∠3,能否判断AB∥CD?说明你的理由. 如图,直线y1=k1x+b和直线y2=k2x+b分别与x轴交于A(-1,0)和B(3,0)两点.则不等式组k1x+b>k2x+b>0的解集为0<x<3.
如图,直线y1=k1x+b和直线y2=k2x+b分别与x轴交于A(-1,0)和B(3,0)两点.则不等式组k1x+b>k2x+b>0的解集为0<x<3.