题目内容
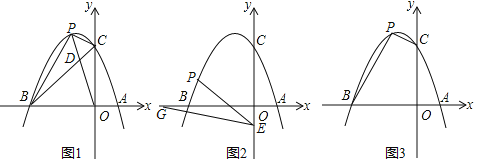
【题目】已知二次函数![]() 图象的顶点坐标为(3,8),该二次函数图像的对称轴与
图象的顶点坐标为(3,8),该二次函数图像的对称轴与![]() 轴的交点为A,M是这个二次函数图像上的点,
轴的交点为A,M是这个二次函数图像上的点,![]() 是原点
是原点
(1)不等式![]() 是否成立?请说明理由;
是否成立?请说明理由;
(2)设![]() 是△AMO的面积,求满足
是△AMO的面积,求满足![]() 的所有点M的坐标.
的所有点M的坐标.
(3)将(2)中符号条件的点M联结起来构成怎样的特殊图形?写出两条这个特殊图形的性质.
【答案】(1)成立,理由见解析;(2)![]()
![]() ;(3)这是一个等腰梯形,性质1:等腰梯形同一底的两个底角相等;性质2:等腰梯形是一个轴对称图形.
;(3)这是一个等腰梯形,性质1:等腰梯形同一底的两个底角相等;性质2:等腰梯形是一个轴对称图形.
【解析】
(1)求出函数解析式,确定b,c的值,即可做出判断;
(2)表示出点A、M坐标,根据三角形面积公式计算即可;
(3)连接四个点,结合四个点的坐标以及抛物线的轴对称性即可得.
(1)由题意得![]() ,
,
![]()
∴![]()
把(3,8)代入![]() 中,解得
中,解得![]()
∴解析式为![]() ,
,
∴![]() ,
,
∴不等式![]() 成立;
成立;
(2)由题意得点A坐标为(3,0),设M(![]() )
)
![]()
即![]()
∴![]()
∴![]()
①当![]()
解得![]()
∴![]()
②当![]()
解得![]()
![]()
∴满足条件的点M的坐标为:![]()
![]() ;
;
(3)如图,顺次链接(2)中四个点,由(2)得M1M2∥M3M4,根据抛物线的对称性得M1M4=M2M3,∴四边形M1M2M3M4是一个等腰梯形,
性质1:等腰梯形同一底的两个底角相等;
性质2:等腰梯形是一个轴对称图形.


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目