题目内容
如图所示，在一座大厦（图中BC）前面30m的地面上有一盏地灯（图中点A）照射大厦，身高为1.6m的小亮（图中EF）站在大厦和地灯之间，若小亮从现在所处位置径直走向大厦，当他走到距离大厦只有5m的D处时停下．（1）请你在图中画出此时小亮的位置及他在地灯A照射下投在大厦BC上的影子．（用线段表示）
（2）请你求出此时小亮在地灯A照射下投在大厦BC上的影长．
考点：相似三角形的应用,中心投影
专题：
分析：（1）根据中心投影的概念进而得出答案；
（2）利用相似三角形的判定方法得出△ADN∽△ABM，即可得出
=
，进而求出即可．
（2）利用相似三角形的判定方法得出△ADN∽△ABM，即可得出
| AD |
| AB |
| DN |
| BM |
解答：
解：（1）如图所示：BM即为所求；
（2）∵DN∥BC，
∴△ADN∽△ABM，
∴
=
，
∵AB=30m，BD=5m，DN=1.6m，则AD=25m，
∴
=
，
解得：BM=1.92，
答：此时小亮在地灯A照射下投在大厦BC上的影长为1.92m．
解：（1）如图所示：BM即为所求；（2）∵DN∥BC，
∴△ADN∽△ABM，
∴
| AD |
| AB |
| DN |
| BM |
∵AB=30m，BD=5m，DN=1.6m，则AD=25m，
∴
| 25 |
| 30 |
| 1.6 |
| BM |
解得：BM=1.92，
答：此时小亮在地灯A照射下投在大厦BC上的影长为1.92m．
点评：此题主要考查了相似三角形的判定与性质，得出△ADN∽△ABM是解题关键．
练习册系列答案
天天向上口算本系列答案
相关题目
如图，在△ABC中，点D是AC上一点，添加下列哪个条件不能得到△CBD∽△CAB的是（ ）| A、∠CDB=∠CBA |
| B、∠CBD=∠A |
| C、BC•AB=BD•AC |
| D、BC2=CD•AC |
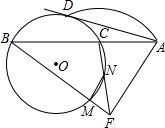已知：如图，AD切⊙O于点D，ACB为⊙O的割线，AP=AD，BP、CP分别交⊙O于M、N．求证：