Question

1．如图，AD⊥BC于点D，∠B=∠DAC，点E在BC上，△EAC是以EC为底的等腰三角形，AB=4，AE=3．
（1）判断△ABC的形状；
（2）求△ABC的面积．

Answer 1

分析 （1）根据AD⊥BC，∠B=∠DAC，求得∠BAC的度数即可；
（2）先根据△EAC是等腰三角形，得出AC=AE=3，再计算△ABC的面积．

解答 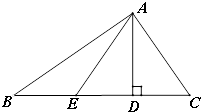解：（1）△ABC是直角三角形；
证明∵AD⊥BC，
∴∠ADB=90°，
∴∠B+∠BAD=90°，
∵∠B=∠DAC，
∴∠DAC+∠BAD=90°，即∠BAC=90°，
∴△ABC是直角三角形；

（2）∵△EAC是等腰三角形，
∴AC=AE=3，
∴△ABC的面积=$\frac{1}{2}$×AB×AC=$\frac{1}{2}$×4×3=6．

点评 本题主要考查了等腰三角形的性质，解题时注意：等腰三角形的两条腰相等，等腰三角形具有三线合一的性质．