题目内容
4．定义一个新的运算：a⊕b=$\left\{\begin{array}{l}-2a+b（a≤b）\\ \frac{b+2}{-a}（a＞b）\end{array}$，则运算x⊕2的最小值为（ ）| A． | -3 | B． | -2 | C． | 2 | D． | 3 |
分析 分x≤2和x＞2两种情况分类讨论得到有关x的函数关系式，求得最小值即可．
解答 解：当x≤2时，x⊕2=-2x+2，
此时当x=2时有最小值-2；
当x＞2时，x⊕2=$\frac{2+2}{-x}$=-$\frac{4}{x}$，
此时没有最小值，
综上，最小值为-2，
故选B．
点评 本题考查了反比例函数的性质及一次函数的性质，解题的关键是能够根据题意得到函数关系式，难度不大．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
15．下列运算正确的是（ ）
| A． | $3+\sqrt{2}=3\sqrt{2}$ | B． | ${2^{-2}}=-\frac{1}{4}$ | C． | $（\sqrt{2}+1）（\sqrt{2}-1）=1$ | D． | 36÷33=32 |
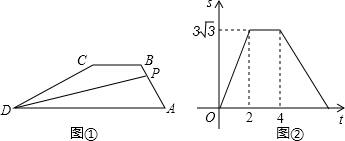
用圆规和直尺作图：已知∠α和线段a，求作△ABC，使∠A=∠α，AB=a，AC=2a．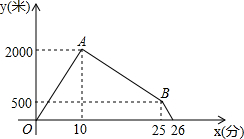
琪琪周日早晨8：00之前要赶到距家8000米的烈士陵园去扫墓，她早上7：20出发，10分钟后父亲发现她忘了带演讲稿，于是立即出发，按琪琪走得路线去追，父亲出发几分钟后，琪琪也发现忘记了带演讲稿，于是立即原路返回去取，1分钟后与父亲相遇，然后父亲立即返回，琪琪赶往陵园．已知父女二人速度始终不变，如图给出了两人之间的距离S（米）和琪琪行驶时间t （分）之间的函数图象．