题目内容
20.解方程:$\frac{{x}^{2}-4}{x+1}$=3-$\frac{3}{x+1}$.分析 分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:去分母得:x2-4=3x+3-3,
整理得:x2-3x-4=0,即(x-4)(x+1)=0,
解得:x=4或x=-1,
经检验x=-1是增根,分式方程的解为x=4.
点评 此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
相关题目
10.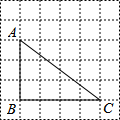 如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则sinA=( )
如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则sinA=( )
 如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则sinA=( )
如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则sinA=( )| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
9.计算:$\sqrt{8}$-$\frac{1}{8}$$\sqrt{48}$-($\frac{2}{3}$$\sqrt{\frac{11}{12}}$-3$\sqrt{\frac{3}{4}}$)
2.一个长方形的周长是26cm,若这个长方形的长减少1cm,宽增加2cm,就可以成为一个正方形,则长方形的长是( )
| A. | 5cm | B. | 7cm | C. | 8cm | D. | 9cm |
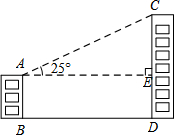 如图,甲楼AB的高度为35m,经测得,甲楼的底端B处与乙楼的底端D处相距105m,从甲楼顶部A处看乙楼顶部C处的仰角∠CAE的度数为25°.求乙楼CD的高度(结果精确到0.1m).[参考数据:sin25°=0.42,cos25°=0.91,tan25°=0.47].
如图,甲楼AB的高度为35m,经测得,甲楼的底端B处与乙楼的底端D处相距105m,从甲楼顶部A处看乙楼顶部C处的仰角∠CAE的度数为25°.求乙楼CD的高度(结果精确到0.1m).[参考数据:sin25°=0.42,cos25°=0.91,tan25°=0.47].