题目内容
6.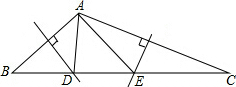 如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E.
如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E.(1)若△ADE周长是10,则BC=10;
(2)若∠BAC=128°,则∠DAE=76°.
分析 (1)由在△ABC中,边AB、AC的垂直平分线分别交BC于E、F,易得AE=BE,AF=CF,即可得BC=△AEF周长;
(2)由∠BAC=128°,可求得∠B+∠C的值,即可得∠BAE+∠CAF的值,继而求得答案.
解答 解:(1)∵在△ABC中,边AB、AC的垂直平分线分别交BC于E、F,
∴AE=BE,AF=CF,
∵△ADE周长是10,
∴BC=BE+EF+CF=AE+EF+AF=10;
故答案为:10;
(2)∵AE=BE,AF=CF,
∴∠B=∠BAE,∠C=∠CAF,
∵∠BAC=128°,
∴∠B+∠C=180°-∠BAC=52°,
∴∠BAE+∠CAF=∠B+∠C=52°,
∴∠FAE=∠BAC-(∠BAE+∠CAF)=76°,
故答案为:76°
点评 此题考查了线段垂直平分线的性质以及等腰三角形的性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
16. 如图,⊙O的直径AB=8,∠CBD=30°,则CD等于( )
如图,⊙O的直径AB=8,∠CBD=30°,则CD等于( )
 如图,⊙O的直径AB=8,∠CBD=30°,则CD等于( )
如图,⊙O的直径AB=8,∠CBD=30°,则CD等于( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
14.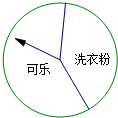 某商场“五一”期间为进行有奖销售活动,设立了一个可以自由转动的转盘.商场规定:顾客购物100元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.下表是此次活动中的一组统计数据:
某商场“五一”期间为进行有奖销售活动,设立了一个可以自由转动的转盘.商场规定:顾客购物100元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.下表是此次活动中的一组统计数据:
(1)完成上述表格;(结果全部精确到0.1)
(2)请估计当n很大时,频率将会接近0.6,假如你去转动该转盘一次,你获得“可乐”的概率约是0.6;(结果全部精确到0.1)
(3)转盘中,表示“洗衣粉”区域的扇形的圆心角约是多少度?
 某商场“五一”期间为进行有奖销售活动,设立了一个可以自由转动的转盘.商场规定:顾客购物100元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.下表是此次活动中的一组统计数据:
某商场“五一”期间为进行有奖销售活动,设立了一个可以自由转动的转盘.商场规定:顾客购物100元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.下表是此次活动中的一组统计数据:| 转动转盘的次数n | 100 | 200 | 400 | 500 | 800 | 1000 |
| 落在“可乐”区域的次数m | 60 | 122 | 240 | 298 | 604 | |
| 落在“可乐”区域的频率$\frac{m}{n}$ | 0.6 | 0.61 | 0.6 | 0.59 | 0.604 |
(2)请估计当n很大时,频率将会接近0.6,假如你去转动该转盘一次,你获得“可乐”的概率约是0.6;(结果全部精确到0.1)
(3)转盘中,表示“洗衣粉”区域的扇形的圆心角约是多少度?
1.在下列性质中,菱形具有而矩形不具有的性质是( )
| A. | 内角和等于360° | B. | 对角相等 | ||
| C. | 对角线平分一组对角 | D. | 邻角互补 |
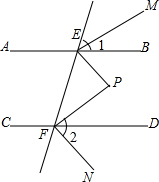 如图,AB∥CD,直线EF分别交AB,CD于点E,F,∠BEF的平分线与∠DFE的平分线相交于点P.∠1与∠2的平分线EM,FN,判断EM,FN所在的直线有什么位置关系,并说明理由.
如图,AB∥CD,直线EF分别交AB,CD于点E,F,∠BEF的平分线与∠DFE的平分线相交于点P.∠1与∠2的平分线EM,FN,判断EM,FN所在的直线有什么位置关系,并说明理由.