题目内容
20．
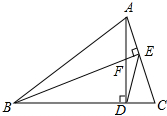如图，AD⊥BC，垂足为D，BE⊥AC，垂足为E，AD与BE相交于点F，连接DE．（1）求证：△AEF∽△BDF；
（2）若∠ABE=m°，求∠ADE的度数（用含m的式子表示）
分析 （1）由AD⊥BC，BE⊥AC，得到∠AEF=∠ADB=90°，根据对顶角相等得到∠AFE=∠DFB，于是得到结论．
（2）由∠AEF=∠ADB=90°，推出A，B，D，E四点共圆，根据圆周角定理即可得到结论．
解答 解：（1）∵AD⊥BC，BE⊥AC，
∴∠AEF=∠ADB=90°，
∵∠AFE=∠DFB，
∴△AEF∽△BDF；
（2）∵∠AEF=∠ADB=90°，
∴A，B，D，E四点共圆，
∴∠ADE=∠ABE=m°．
点评 本题考查了相似三角形的判定，四点共圆，垂直的定义，熟练掌握相似三角形的判定定理是解题的关键．
练习册系列答案
相关题目
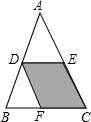如图，在△ABC中，D、E分别是边AB、AC的中点，连接DE，将△ADE沿AB方向平移到△DBF的位置，点D在BC上，已知△ADE的面积为1，则四边形CEDF的面积是2．
在平面直角坐标系中有一个正方形OACB，点A坐标为（4，0），M、N分别是OA、AC上的两个动点，当M点在OA上运动时，一直保持BM和MN垂直．