题目内容
5.(1)计算:($\frac{3}{4}$)0-4sin45°tan45°+($\frac{1}{2}$)-1+(-1)2015+$\sqrt{9}$(2)先化简,再求值:${b^2}-\frac{{{a^3}-a{b^2}}}{a+b}÷({a-\frac{{ab-{b^2}}}{a-b}})$,其中a=-1,b=2.
分析 (1)根据零指数幂、特殊角的三角函数、负整数指数幂、-1的奇数次方、求算术平方根,可以将原式化简,然后再合并同类项即可解答本题;
(2)先将原式分解因式的先分解因式,然后再约分即可对原式进行化简,然后将a=-1,b=2代入化简后的式子即可解答本题.
解答 解:(1)($\frac{3}{4}$)0-4sin45°tan45°+($\frac{1}{2}$)-1+(-1)2015+$\sqrt{9}$
=1-4×$\frac{\sqrt{2}}{2}×1+2+(-1)+3$
=1-2$\sqrt{2}+2+(-1)+3$
=5-2$\sqrt{2}$;
(2)${b^2}-\frac{{{a^3}-a{b^2}}}{a+b}÷({a-\frac{{ab-{b^2}}}{a-b}})$
=${b}^{2}-\frac{a({a}^{2}-{b}^{2})}{a+b}÷\frac{a(a-b)-(ab-{b}^{2})}{a-b}$
=${b}^{2}-\frac{a(a+b)(a-b)}{a+b}×\frac{a-b}{{a}^{2}-ab-ab+{b}^{2}}$
=${b}^{2}-a(a-b)×\frac{a-b}{(a-b)^{2}}$
=b2-a,
当a=-1,b=2时,原式=b2-a=22-(-1)=4+1=5.
点评 本题考查分式的化简求值、实数的运算、零指数幂、负整数指数幂、特殊角的三角函数值,解题的关键是明确它们各自的计算方法.

练习册系列答案
相关题目
15.下列说法正确的是( )
| A. | 整数包括正整数和负整数 | B. | 0是整数但不是正数 | ||
| C. | 正数,负数,0统称为有理数 | D. | 非负有理数是指正有理数 |
13.若-5是一元二次方程x2-9x+m=0的一个根,则方程的另一根是( )
| A. | 4 | B. | -4 | C. | 14 | D. | -14 |
10.2015年4月某日我市区县的可吸入颗粒物数值统计如下表:
该日这一时刻的可吸入颗粒物数值的众数和中位数分别是( )
| 区县 | 宣威 | 富源 | 沾益 | 马龙 | 师宗 | 罗平 | 陆良 | 会泽 | 麒麟区 | 经开区 |
| 可吸入颗粒物 (mg/m3) | 0.18 | 0.18 | 0.15 | 0.13 | 0.14 | 0.13 | 0.15 | 0.15 | 0.15 | 0.14 |
| A. | 0.15和0.14 | B. | 0.18和0.15 | C. | 0.18和0.14 | D. | 0.15和0.15 |
15.在平面直角坐标系xOy中,点P(5,-2)关于x轴的对称点的坐标是( )
| A. | (-5,-2) | B. | (5,2) | C. | (-5,2) | D. | (2,5) |

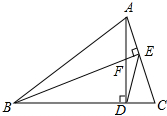 如图,AD⊥BC,垂足为D,BE⊥AC,垂足为E,AD与BE相交于点F,连接DE.
如图,AD⊥BC,垂足为D,BE⊥AC,垂足为E,AD与BE相交于点F,连接DE.