题目内容
18.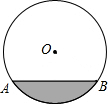 一圆柱形排水管的截面如图所示,已知排水管的半径为1m,水面宽AB为1.6m.由于天气干燥,水管水面下降,此时排水管水面宽变为1.2m,求水面下降的高度.
一圆柱形排水管的截面如图所示,已知排水管的半径为1m,水面宽AB为1.6m.由于天气干燥,水管水面下降,此时排水管水面宽变为1.2m,求水面下降的高度.
分析 先根据垂径定理求得AM、CN,然后根据勾股定理求出OM、ON的长,即可得出结论.
解答 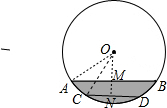 解:如图,下降后的水面宽CD为1.2m,连接OA,OC,过点O作ON⊥CD于N,交AB于M.
解:如图,下降后的水面宽CD为1.2m,连接OA,OC,过点O作ON⊥CD于N,交AB于M.
∴∠ONC=90°.
∵AB∥CD,
∴∠OMA=∠ONC=90°.
∵AB=1.6,CD=1.2,
∴AM=$\frac{1}{2}$AB=0.8,CN=$\frac{1}{2}$CD=0.6,
在Rt△OAM中,
∵OA=1,
∴OM=$\sqrt{O{A}^{2}-A{M}^{2}}$=0.6.
同理可得ON=0.8,
∴MN=ON-OM=0.2(米).
答:水面下降了0.2米.
点评 本题考查的是垂径定理的应用以及勾股定理的应用,熟知平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧是解答此题的关键.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
13. 如图,△ABC内接于⊙O,BD是⊙O的直径.若∠DBC=33°,则∠A等于( )
如图,△ABC内接于⊙O,BD是⊙O的直径.若∠DBC=33°,则∠A等于( )
 如图,△ABC内接于⊙O,BD是⊙O的直径.若∠DBC=33°,则∠A等于( )
如图,△ABC内接于⊙O,BD是⊙O的直径.若∠DBC=33°,则∠A等于( )| A. | 33° | B. | 57° | C. | 67° | D. | 66° |
 如图,在平面直角坐标系中,
如图,在平面直角坐标系中, 如图是小明制作的一个轴对称图形风筝,已知OC是对称轴,∠A=35°,∠BCO=30°,则∠AOC=115°.
如图是小明制作的一个轴对称图形风筝,已知OC是对称轴,∠A=35°,∠BCO=30°,则∠AOC=115°. 如图是由八个相同的小正方体组合而成的几何体,从正面看到的图形是( )
如图是由八个相同的小正方体组合而成的几何体,从正面看到的图形是( )



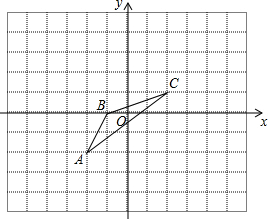
 如图,在平面直角坐标系中,直线y=$\frac{1}{2}$x+2与x轴、y轴分别交于A、B两点,以AB为边在第二象限内作正方形ABCD.
如图,在平面直角坐标系中,直线y=$\frac{1}{2}$x+2与x轴、y轴分别交于A、B两点,以AB为边在第二象限内作正方形ABCD.