题目内容
5.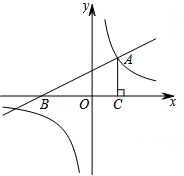 如图,一次函数y=$\frac{1}{2}$x+2的图象与x轴交于点B,与反比例函数y=$\frac{k}{x}$的图象的一个交点为A(2,m).
如图,一次函数y=$\frac{1}{2}$x+2的图象与x轴交于点B,与反比例函数y=$\frac{k}{x}$的图象的一个交点为A(2,m).(1)求反比例函数的表达式;
(2)求当x满足什么范围时,$\frac{1}{2}$x+2<$\frac{k}{x}$;
(3)过点A作AC⊥x轴,垂足为点C,如果点P在反比例函数图象上,且△PBC的面积等于6,请直接写出点P的坐标.
分析 (1)先将点A(2,m)代入反比例函数y=$\frac{1}{2}$x+2求得A的坐标,然后代入y=$\frac{k}{x}$,求得k的值即可;
(2)首先求出两函数交点的坐标,再结合反比例函数和一次函数的图象即可求出$\frac{1}{2}$x+2<$\frac{k}{x}$的解集;
(3)可求得点B的坐标,设P(x,y),由S△PBC=6,即可求得x,y的值.
解答 解:(1)∵一次函数y=$\frac{1}{2}$x+2的图象经过点A(2,m),
∴m=3.
∴点A的坐标为(2,3).
∵反比例函数y=$\frac{k}{x}$的图象经过点A(2,3),
∴k=6,
∴反比例函数的表达式为y=$\frac{6}{x}$.
(2)联立反比例函数和一次函数的解析式得:
$\left\{\begin{array}{l}{y=\frac{1}{2}x+2}\\{y=\frac{6}{x}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$或$\left\{\begin{array}{l}{x=-6}\\{-1}\end{array}\right.$,
∴$\frac{1}{2}$x+2<$\frac{k}{x}$的解集为:x<-6或0<x<2;
(3)令$\frac{1}{2}$x+2=0,解得x=-4,即B(-4,0),
∵AC⊥x轴,
∴C(2,0).
∴BC=6.
设P(x,y),
∵S△PBC=$\frac{1}{2}$•BC•|y|=6,
∴y1=2或y2=-2.
分别代入y=$\frac{6}{x}$中,
得x1=3或x2=-3.
∴P(3,2)或P(-3,-2).
点评 本题考查了一次函数和反比例函数的交点问题,利用待定系数法求解析式是解此题的关键.

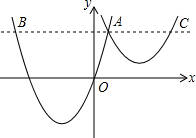 如图,抛物线y1=a(x+2)2-3与y2=$\frac{1}{2}$(x-3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论:①无论x取何值,y2的值总是正数;②a=$\frac{2}{3}$;③当x=0时,y2-y1=6;④AB+AC=10;其中正确结论的个数是( )
如图,抛物线y1=a(x+2)2-3与y2=$\frac{1}{2}$(x-3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论:①无论x取何值,y2的值总是正数;②a=$\frac{2}{3}$;③当x=0时,y2-y1=6;④AB+AC=10;其中正确结论的个数是( )| A. | ①②④ | B. | ①③④ | C. | ②③④ | D. | ①②③④ |
| 货物 | 上衣 (件) | 裤子 (条) | 鞋子 (双) |
| 3天的销售总量 | 72 | 30 | 15 |
(2)把表格补充完整.
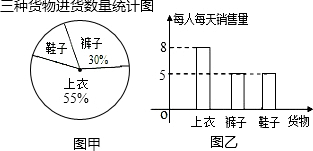
(3)若销售人员不变,以同样的销售速度销售,请通过计算说明哪种货物最先售完?
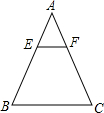 如图,在△ABC中,EF∥BC,$\frac{AE}{EB}$=$\frac{1}{3}$,S四边形BCFE=15,则S△ABC=16.
如图,在△ABC中,EF∥BC,$\frac{AE}{EB}$=$\frac{1}{3}$,S四边形BCFE=15,则S△ABC=16.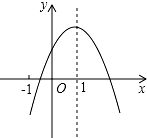 如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc<0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤a+b<m (am+b)(m≠1的实数).其中正确结论的有( )
如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc<0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤a+b<m (am+b)(m≠1的实数).其中正确结论的有( )