题目内容
11.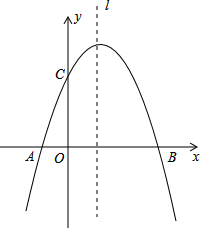 已知:抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴,M为它的顶点
已知:抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴,M为它的顶点(1)求抛物线的函数关系式;
(2)求△MCB的面积;
(3)设点P是直线l上的一个动点,当PA+PC最小时,求点P的坐标.
分析 (1)根据待定系数法求出抛物线解析式;
(2)先求出直线BC与对称轴的交点,即可得出MN,再用面积之和即可得出结论;
(3)先根据抛物线的对称性,判断出点P是直线BC与抛物线的对称轴l的交点,根据(2)直接得出点P坐标.
解答 解:(1)∵抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,
∴$\left\{\begin{array}{l}{a-b+c=0}\\{9a+3a+c=0}\\{c=3}\end{array}\right.$,
∴$\left\{\begin{array}{l}{a=-1}\\{b=2}\\{c=3}\end{array}\right.$,
∴抛物线的函数关系式为y=-x2+2x+3;
(2)如图1,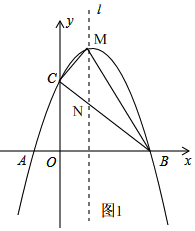
由(1)知,抛物线的函数关系式为y=-x2+2x+3;
∴抛物线的对称轴为x=1,M(1,4),
∵B(3,0)、C(0,3),
∴直线BC解析式为y=-x+3,
当x=1时,y=2,
∴N(1,2).
∴MN=2,OB=3,
∴S△MCB=S△MNC+S△MNB=$\frac{1}{2}$MN×OB=$\frac{1}{2}$×2×3=3;
(3)如图2,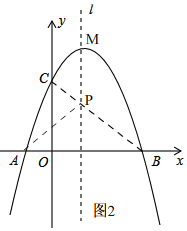 ∵直线l是抛物线的对称轴,且A,B是抛物线与x轴的交点,
∵直线l是抛物线的对称轴,且A,B是抛物线与x轴的交点,
∴点A,B关于直线l对称,
∴PA+PC最小时,点P就是直线BC与直线l的交点,
由(2)知,抛物线与直线BC的交点坐标为(1,2),
∴点P(1,2).
点评 此题是二次函数综合题,主要考查了待定系数法,三角形的面积的计算方法,对称的性质,解本题的关键是确定出抛物线的解析式,是一道比较简单数形结合的试题.

练习册系列答案
相关题目
1.3的算术平方根是( )
| A. | 9 | B. | $\sqrt{3}$ | C. | -9 | D. | -$\sqrt{3}$ |
19. 如图,在半径为5cm的⊙O中,弦AB=8cm,OC⊥AB于点C,则OC=( )
如图,在半径为5cm的⊙O中,弦AB=8cm,OC⊥AB于点C,则OC=( )
 如图,在半径为5cm的⊙O中,弦AB=8cm,OC⊥AB于点C,则OC=( )
如图,在半径为5cm的⊙O中,弦AB=8cm,OC⊥AB于点C,则OC=( )| A. | 3cm | B. | 4cm | C. | 5cm | D. | 6cm |
6.下列说法中错误的是( )
| A. | 正分数、负分数统称分数 | B. | 零是整数,但不是分数 | ||
| C. | 正整数、负整数统称整数 | D. | 零既不是正数,也不是负数 |
16.下列是一元二次方程的有多少个( )
①(x+1)(x-2)=3;②ax2+bx+c=0;③3(x-1)2=3x2+2x;④$\sqrt{{x}^{2}}$-1=0;⑤x2+y+4=0.
①(x+1)(x-2)=3;②ax2+bx+c=0;③3(x-1)2=3x2+2x;④$\sqrt{{x}^{2}}$-1=0;⑤x2+y+4=0.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
20.已知点M到x轴、y轴的距离分别为4和6,且点M在x轴的上方、y轴的左侧,则点M的坐标为( )
| A. | (4,-6) | B. | (-4,6) | C. | (6,-4) | D. | (-6,4) |
1.在函数y=$\sqrt{x+2}$中,自变量x的取值范围是( )
| A. | x≥2 | B. | x≥-2 | C. | x>2 | D. | x>-2 |
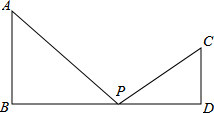 如图所示,AB⊥BD,CD⊥BD,AB=6,CD=4,BD=k,点P在BD上移动,保持∠APC=90°,但不与点B和点D重合.
如图所示,AB⊥BD,CD⊥BD,AB=6,CD=4,BD=k,点P在BD上移动,保持∠APC=90°,但不与点B和点D重合.