题目内容
 如图,O是矩形ABCD的对角线AC、BD的交点,OM⊥AD,垂足为M,若AB=6,则OM长为
如图,O是矩形ABCD的对角线AC、BD的交点,OM⊥AD,垂足为M,若AB=6,则OM长为考点:三角形中位线定理,矩形的性质
专题:
分析:首先根据矩形的性质可得O为BD中点,再证明△DMO∽△DAB可得
=
=
,代入AB的值可得答案.
| MO |
| AB |
| DO |
| BD |
| 1 |
| 2 |
解答:解:∵四边形ABCD是矩形,
∴O为BD中点,∠BAD=90°,
∵OM⊥AD,
∴∠DMO=90°,
∴AB∥MO,
∴△DMO∽△DAB,
∴
=
=
,
∵AB=6,
∴MO=3,
故答案为:3.
∴O为BD中点,∠BAD=90°,
∵OM⊥AD,
∴∠DMO=90°,
∴AB∥MO,
∴△DMO∽△DAB,
∴
| MO |
| AB |
| DO |
| BD |
| 1 |
| 2 |
∵AB=6,
∴MO=3,
故答案为:3.
点评:此题主要考查了矩形的性质,以及相似三角形的判定与性质,关键是掌握相似三角形对应边成比例.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
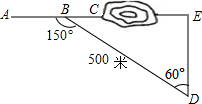 如图,沿AC方向开山修路,为了加快施工进度,要在小山的另一边同时施工,从AC上的一点B,取∠ABD=150°,BD=500米,∠D=60°.要使A,C,E成一直线.那么开挖点E离点D的距离是( )
如图,沿AC方向开山修路,为了加快施工进度,要在小山的另一边同时施工,从AC上的一点B,取∠ABD=150°,BD=500米,∠D=60°.要使A,C,E成一直线.那么开挖点E离点D的距离是( )| A、200米 | B、250米 |
| C、300米 | D、350米 |
 如图,过A、B、C、D、E五个点中任意三点画三角形,
如图,过A、B、C、D、E五个点中任意三点画三角形,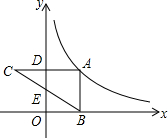 如图,点A在反比例函数y=
如图,点A在反比例函数y= 如图,是变压器中的L型硅钢片,其面积为
如图,是变压器中的L型硅钢片,其面积为