题目内容
18．已知一元二次方程x2-2x-1=0的两根分别为m、n，则m+n的值为（ ）| A． | -2 | B． | -1 | C． | 1 | D． | 2 |
分析 根据一元二次方程的系数结合根与系数的关系即可得出m+n的值，由此即可得出结论．
解答 解：∵方程x2-2x-1=0的两根分别为m、n，
∴m+n=-$\frac{b}{a}$=2．
故选D．
点评 本题考查了根与系数的关系，解题的关键是找出m+n=2．本题属于基础题，难度不大，解决该题型题目时，利用根与系数的关系找出两根之和与两根之积是关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
8．某煤矿原计划x天生存120t煤，由于采用新的技术，每天增加生存3t，因此提前2天完成，列出的方程为（ ）
| A． | $\frac{120}{x-2}$=$\frac{120}{x}$=-3 | B． | $\frac{120}{x}=\frac{120}{x+2}$-3 | C． | $\frac{120}{x+2}=\frac{120}{x}$-3 | D． | $\frac{120}{x}$=$\frac{120}{x-2}$-3 |
13．如果盈利20元记作+20，那么亏本50元记作（ ）
| A． | +50元 | B． | -50元 | C． | +20元 | D． | -20元 |
实数a、b在数轴上的位置如图所示，则化简 $\sqrt{{{（-a）}^2}}+\sqrt{b^2}-\sqrt{{{（a+b）}^2}}$的结果为2b．
10．八年级学生去距学校11km的科技馆参观，一部分学生骑自行车，过了20min后，其余学生乘汽车出发，结果他们同时到达．已知汽车的速度是骑车学生速度的2倍，求骑车学生的速度，设骑车学生的速度为xkm/h，则所列方程正确的是（ ）
| A． | $\frac{11}{x}=\frac{11}{2x}-\frac{1}{3}$ | B． | $\frac{11}{x}=\frac{11}{2x}-20$ | C． | $\frac{11}{x}=\frac{11}{2x}+\frac{1}{3}$ | D． | $\frac{11}{x}=\frac{11}{2x}+20$ |
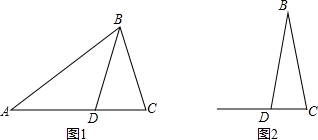小明在做数学练习时，遇到下面的题目：