题目内容
7.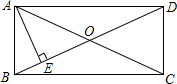 如图,在矩形ABCD中,AE⊥BD于E,∠DAE=3∠BAE,则∠EAC为( )
如图,在矩形ABCD中,AE⊥BD于E,∠DAE=3∠BAE,则∠EAC为( )| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
分析 由矩形的性质得出OA=OB,∠OAB=∠OBA,由已知条件得出∠BAE=22.5°,由角的互余关系求出∠OBA,得出∠OAB,即可求出∠EAC的度数.
解答 解:∵四边形ABCD是矩形,
∴∠BAD=90°,OA=$\frac{1}{2}$AC,OB=$\frac{1}{2}$BD,AC=BD,
∴OA=OB,
∴∠OAB=∠OBA,
∵∠DAE=3∠BAE,
∴∠BAE=$\frac{1}{4}$∠BAD=$\frac{1}{4}$×90°=22.5°,
∵AE⊥BD,
∴∠AEB=90°,
∴∠OBA=90°-22.5°=67.5°,
∴∠OAB=67.5°,
∴∠EAC=67.5°-22.5°=45°;
故选:B.
点评 本题考查了矩形的性质、等腰三角形的性质、角的互余关系;熟练掌握矩形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
15.计算a2(a+b)(a-b)+a2b2等于( )
| A. | a2b2 | B. | a6 | C. | a4 | D. | a2b2 |
19. 在?ABCD中,∠ACB=25°,现将?ABCD沿EF折叠,使点C与点A重合,点D落在G处,则∠GFE的度数( )
在?ABCD中,∠ACB=25°,现将?ABCD沿EF折叠,使点C与点A重合,点D落在G处,则∠GFE的度数( )
 在?ABCD中,∠ACB=25°,现将?ABCD沿EF折叠,使点C与点A重合,点D落在G处,则∠GFE的度数( )
在?ABCD中,∠ACB=25°,现将?ABCD沿EF折叠,使点C与点A重合,点D落在G处,则∠GFE的度数( )| A. | 135° | B. | 120° | C. | 115° | D. | 100° |
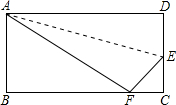 如图,在矩形ABCD中,已知AB=6cm,BC=10cm,折叠矩形的一边AD,使点D落在BC边上的点F处,折痕为AE,求CE的长.
如图,在矩形ABCD中,已知AB=6cm,BC=10cm,折叠矩形的一边AD,使点D落在BC边上的点F处,折痕为AE,求CE的长. 如图:在Rt△ABC中,∠C为直角,CD⊥AB于点D,BC=3,AB=5,写出其中的一对相似三角形是△ABC 和△CBD.
如图:在Rt△ABC中,∠C为直角,CD⊥AB于点D,BC=3,AB=5,写出其中的一对相似三角形是△ABC 和△CBD.