题目内容
16．
如图：在Rt△ABC中，∠C为直角，CD⊥AB于点D，BC=3，AB=5，写出其中的一对相似三角形是△ABC 和△CBD．
分析 因为直角三角形斜边上的高，把直角三角形分成的两个三角形与原三角形相似．
解答 解：∵∠C=90°，CD⊥AB
∴∠CDB=∠ACB=90°，
∵∠B=∠B，
∴△ABC∽△CBD，
故答案为：△ABC和△CBD．
点评 此题主要考查的是相似三角形的判定，找准相似三角形的对应边是解题的关键．
练习册系列答案
相关题目
6．在反比例函数$y=\frac{3}{x}$图象上的点是（ ）
| A． | （1，3） | B． | （-1，3） | C． | （1，-3） | D． | $（{\frac{1}{3}，1}）$ |
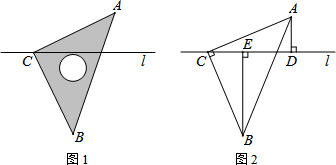
7．
如图，在矩形ABCD中，AE⊥BD于E，∠DAE=3∠BAE，则∠EAC为（ ）
如图，在矩形ABCD中，AE⊥BD于E，∠DAE=3∠BAE，则∠EAC为（ ）| A． | 30° | B． | 45° | C． | 60° | D． | 75° |
如图，在?ABCD中，E是AD边上的中点，连接BE并延长与CD的延长线交于点F．证明：AB=DF．
已知：如图，CD⊥AB，GF⊥AB，∠B=∠ADE，求证：∠1=∠2．
1．
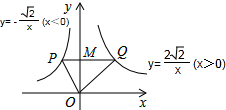函数y=-$\frac{\sqrt{2}}{x}$（x＜0）和y=$\frac{2\sqrt{2}}{x}$（x＞0）的图象如图所示，O为坐标原点，M是y轴正半轴上任意一点，过点M作PQ∥x轴，分别与图中的函数图象相交于P、Q两点，连接OP、OQ，则△OPQ的面积为（ ）
函数y=-$\frac{\sqrt{2}}{x}$（x＜0）和y=$\frac{2\sqrt{2}}{x}$（x＞0）的图象如图所示，O为坐标原点，M是y轴正半轴上任意一点，过点M作PQ∥x轴，分别与图中的函数图象相交于P、Q两点，连接OP、OQ，则△OPQ的面积为（ ）| A． | $\sqrt{2}$ | B． | $\frac{3}{2}\sqrt{2}$ | C． | 2$\sqrt{2}$ | D． | $\frac{5}{2}\sqrt{2}$ |
